고정 헤더 영역
상세 컨텐츠
본문
헤론의 공식 유도 및 활용에 대한 자세한 이해 (고1수학 다항식의 곱셈 심화)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
이번 포스팅은 다항식의 곱셈에 대한 심화 내용으로 삼각형에서 성립하는 것으로 널리 알려진 헤론의 공식에 대해 다뤄보도록 하겠습니다.

● 들어가기
내용에 들어가기 앞서 다음의 문제를 살펴보겠습니다.
| 세 변의 길이가 각각 $a$, $b$, $c$인 삼각형에서 $a^2+b^2+c^2=10$, $a^4+b^4+c^4=18$이 성립할 때, 이 삼각형의 넓이를 구하시오. |
조건이 등장하는 모양새로 봐서 다항식의 곱셈 공식을 활용해야 할거 같은 문제인데 어떻게 접근해야 할지 막막하죠. 이 문제를 풀기 위해 헤론의 공식이 연관됩니다.
헤론의 공식(Heron's formula)은 고대 그리스 시대의 알렉산드리아 수학자 헤론의 이름을 따서 부르게 된 공식으로 삼각형의 세 변의 길이를 알면 그 넓이를 구하게 해주는 공식으로 다음과 같습니다.

복잡해 보이지만 밑변과 높이를 일일이 찾을 필요 없이 어떠한 삼각형이든 세 변의 길이만으로 넓이를 구해주는 점에서 상당히 유용한 공식이라 볼 수 있습니다. 이렇게 대단한 공식이 고대시대에 이미 정리가 되었다는 점이 놀라운데요. 다항식의 곱셈과 인수분해를 통해 이 공식을 유도할 수 있습니다.
● 헤론의 공식 유도
다음 그림과 같은 삼각형 $\textrm{ABC}$를 생각해 보겠습니다.

점 $\textrm{A}$에서 변 $\textrm{BC}$에 내린 수선의 발을 $\overline{\textrm{AH}}=h$라 하고 라 놓으면 삼각형의 넓이는 $\frac{ah}{2}$가 됩니다. 이제 $h$를 구하기 위해 피타고라스 정리에 의해 다음과 같이 식을 세울 수 있습니다.
$a=\overline{\textrm{BH}}+\overline{\textrm{HC}}=\sqrt{c^2-h^2}+\sqrt{b^2-h^2}$
근호를 풀기 위해 양변을 제곱하고 이항해서 근호가 있는 식과 없는 식을 분리하면

아직 근호가 남아 있으니 여기서 양변을 한 번 더 제곱합니다. 식이 너무 복잡해서 정말 이렇게까지 해야 하는가 싶겠지만 $h$를 구하는 게 목적이니 좌변에서 $h$를 제외한 나머지는 하나로 묶어서 계산해 보겠습니다.

이렇게 했더니 좌변, 우변에 공통 항인 $4h^4$이 소거되고 $h^2$에 대하여 푸는 것이 가능해집니다. 또한 이 식에서 우변 $-4(b^2+c^2)h^2$를 이항하면 좌변의 $4(a^2-b^2-c^2)h^2$와 만나서 $4a^2h^2$을 만드므로 다음과 같이 꽤 간단하게 정리되는 것을 알 수 있습니다.
$4a^2h^2=4b^2c^2-(a^2-b^2-c^2)^2$
그럼 이제 여기에서 양변에 근호를 다시 씌우면 좌변에 $ah$가 만들어지면서 삼각형의 넓이를 유도할 수 있게 됩니다. 우선 우변을 인수분해하여 먼저 정리해 보면

따라서 양변을 16으로 나누고 $s=\frac{a+b+c}{2}$로 놓으면 다음과 같이 정리됩니다.

이 과정은 처음의 예시로 든 삼각형이 예각삼각형임을 전제로 하여 유도한 것이지만, 다음과 같이 둔각삼각형의 경우에도 둔각을 가지는 점에서 마주 보는 변에 수선의 발을 내리면 위와 똑같은 식을 세워서 유도하는 게 가능합니다. 따라서 헤론의 공식은 삼각형이 어떠한 모양이든 세 변의 길이만 주어지면 넓이를 구할 수 있도록 합니다.

유도과정에서 보다시피 근호를 없애기 위해 두 번이나 완전제곱을 하면서 그 과정이 꽤 복잡하므로 고등학교의 정규 교육과정에는 포함되어있지 않습니다. 그러나 나중에 기하를 공부하면 이차곡선 편에서 타원이나 쌍곡선의 방정식을 유도할 때 이와 비슷한 과정을 거치므로 연습 삼아 한 번씩 유도해 볼 필요는 있습니다. 또한, 공식 자체는 써먹을 만하니까 기억하고 있으면 문제 해법의 폭을 넓힐 수 있겠죠.
● 헤론의 공식을 이용한 삼각형의 넓이
예를 들어, 다음의 삼각형을 보겠습니다.

넓이가 얼마인지는 쉽게 구할 수 있죠? 직각삼각형이므로 $\frac{1}{2}$에다가 가로와 세로의 길이를 곱하면 6이 나오지만 헤론의 공식을 이용하면 $s=\frac{3+4+5}{2}=6$이므로
$\sqrt{6\times (6-3)\times (6-4)\times (6-5)}$
$\sqrt{36}=6$
이 되어 똑같이 삼각형의 넓이가 되는 것을 알 수 있습니다. 이렇게 쉬운 삼각형의 경우는 헤론의 공식이 굳이 필요 없겠지만 이 공식은 일반적인 모든 삼각형에 적용할 수 있다는 점이 큰 강점이 됩니다.
● 예제 풀이
이제 처음에 소개한 예제를 풀어보겠습니다.

세 변의 길이가 각각 $a$, $b$, $c$인 삼각형에서 $a^2+b^2+c^2=10$, $a^4+b^4+c^4=18$이 성립할 때, 이 삼각형의 넓이를 구하시오.
문제에서 주어진 두 조건 식을 만족하면 $a$, $b$, $c$가 각각 어떠한 값이든 삼각형의 넓이는 일정하게 나올 거란 예측은 할 수 있어요. 그렇다고 $a$, $b$, $c$에 특정한 값을 넣어서 대입할 수 있을 만큼 간단한 조건은 아니라서 특수화 전략을 쓸 수는 아니지만 삼각형을 적당히 그려보는 건 가능하겠죠. 편의상 위에서 공식을 유도할 때 쓴 삼각형을 다시 활용해 봅시다.

그리고 $\overline{\textrm{AH}}=h$로 놓고 앞에서 유도했던 과정을 그대로 다시 시작합니다.

여기까지 앞의 유도과정과 똑같이 구해줍니다. 이제 문제에서는 식 $a^2+b^2+c^2=10$와 $a^4+b^4+c^4=18$의 값을 제시하고 있으므로 여기서 곱셈 공식으로 우변을 전개하면 해답으로 접근할 수 있습니다.
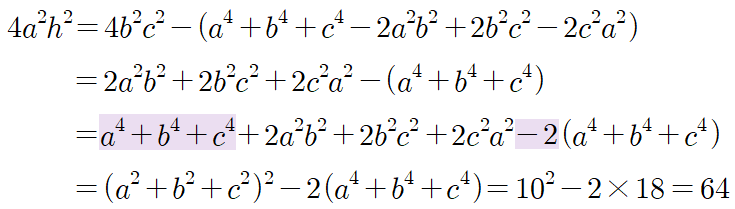
이제 양변을 16으로 나누고 루트를 씌우면 구하는 넓이는

♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 다항식' 카테고리의 다른 글
| 항등식에 대한 자세한 이해 (고1수학 다항식) (0) | 2023.04.19 |
|---|---|
| 다항식의 나눗셈 기본 개념, 원리에 대한 자세한 이해 (고1 수학 다항식) (0) | 2023.03.30 |
| 다항식 곱셈 공식의 다양한 활용 문제에 대한 자세한 해설 (고1 수학 다항식) (0) | 2023.03.09 |
| 다항식의 곱셈 및 곱셈 공식 기억하는 법 (고1 수학 다항식) (0) | 2023.03.05 |
| 다항식의 기본 용어, 오름차순 및 내림차순 정리, 덧셈과 뺄셈 (고1 수학, 다항식) (0) | 2023.03.01 |





댓글 영역