고정 헤더 영역
상세 컨텐츠
본문
집합의 연산 - 합집합과 교집합의 기본 개념 이해 (고1수학 집합과 명제)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
앞선 포스팅에서 집합에 대한 기본 개념을 정리해봤는데 수학에서는 이렇게 새로운 대상을 배우면 늘 다음과 같은 패턴으로 내용을 전개하는 경향이 있습니다. 수학에서 가장 기본이 되는 것이 연산이니까요.
| 새로운 대상 정의 ↓ 새로운 대상의 연산 정의 ↓ 연산 법칙 확인하고 정리 |
따라 오늘의 집합과 명제 포스팅에서는 새롭게 배운 개념인 집합의 연산을 배웁니다. 연산이란 두 개의 대상으로 일정한 규칙에 따라 새로운 하나를 만드는 것이죠. 집합의 연산 또한 두 개의 집합으로 하나의 집합을 만드는 개념입니다.

● 합집합과 교집합의 뜻
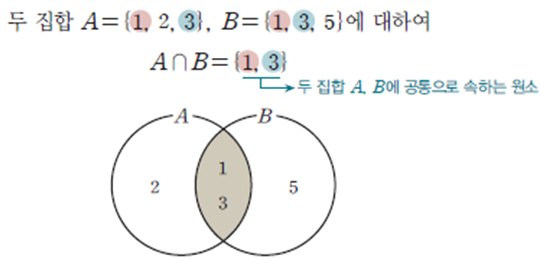
두 집합 $A$, $B$에 대하여 $A$에 속하거나 $B$에 속하는 모든 원소로 이루어진 집합을 $A$와 $B$의 합집합이라 하고, 이것을 기호로 $\mathbf{A\cup B}$와 같이 나타냅니다. 즉, 조건제시법과 벤다이어그램으로 표현한 합집합의 정의는 다음과 같습니다.
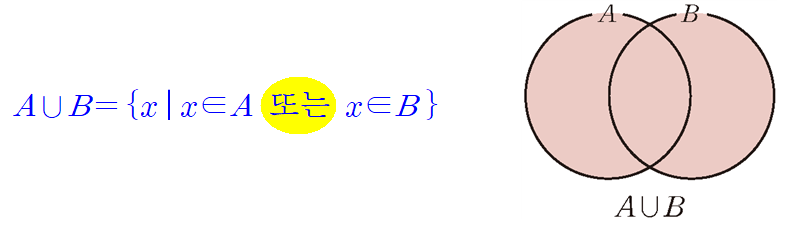
합집합의 '합'은 한자로 合로 여럿을 모은다, 합친다는 의미를 갖습니다. 즉, 합집합은 두 집합 $A$, $B$를 합치는 개념이라 생각할 수 있죠. 기호 $\cup$ 또한 합집합을 의미하는 Union의 앞글자를 따서 만든 것으로 이해하시면 됩니다.
또한, 두 집합 $A$, $B$에 대하여 $A$에도 속하고 $B$에도 속하는 모든 원소로 이루어진 집합을 $A$와 $B$의 교집합이라 하고, 이것을 기호로 $\mathbf{A\cap B}$와 같이 나타냅니다. 즉, 조건제시법과 벤다이어그램으로 표현한 교집합의 정의는 다음과 같습니다.
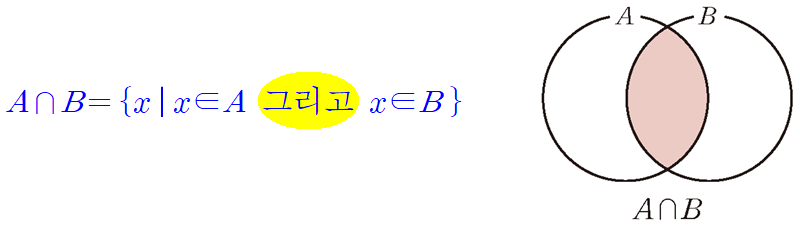
즉, 교집합은 두 집합 $A$, $B$를 겹치는 개념이라 생각할 수 있죠. 교집합의 '교'는 한자로 交(사귈 교)로 교차로의 교와 같은 한자를 씁니다. 기호 $\cap$은 합집합과 반대되는 개념으로 만든 것이나 원소가 두 집합에 양다리를 걸친다는 의미로 이해하셔도 좋습니다.

위의 조건제시법으로 정의한 식에서 합집합은 '또는'과 연결되고 교집합은 '그리고'와 연결되는 개념임을 알 수 있죠. '또는'과 '그리고'는 수학에서 엄청나게 중요한 부사이므로 잘 익혀두시기 바랍니다.
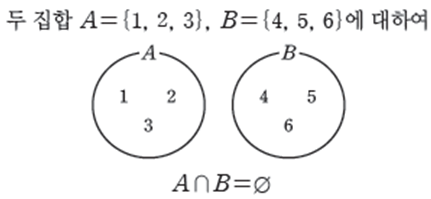
한편, 두 집합 $A$, $B$에서 공통된 원소가 하나도 없을 때 즉, $\mathbf{A\cap B}=\varnothing$이면 $A$와 $B$는 서로소라고 합니다. 벤다이어그램으로 나타내면 다음과 같은 관계죠.
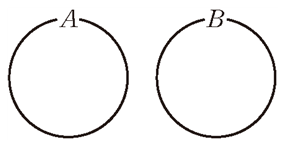
'서로소'라는 용어는 서로 잘 어울리지 못한다는 의미가 있습니다. 자연수에서도 공약수가 1 뿐인 두 자연수를 서로소라고 정의한 적이 있었죠. 집합에서도 원소를 공유하지 않는 두 집합을 서로소라 부릅니다.
지금까지 알아본 내용은 다음과 같은 예시를 통해 정리할 수 있습니다.
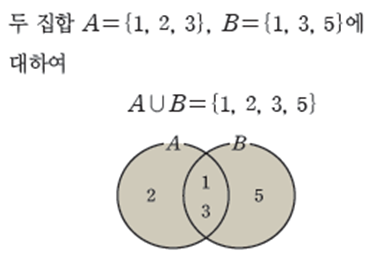
추가적으로 합집합과 교집합은 연산의 정의에 따라 다음이 성립합니다.
$(A\cap B)\subset A\subset (A\cup B)$, $(A\cap B)\subset B\subset (A\cup B)$

두 집합 $A=\left\{1,~3\right\}$, $B=\left\{2,~3,~4,~5\right\}$에 대하여 집합 $A\cup B$의 모든 원소의 합은? [2016.09/2점]
① $14$ ② $15$ ③ $16$ ④ $17$ ⑤ $18$
$A\cup B=\left\{1,~2,~3,~4,~5\right\}$이므로
$1+2+3+4+5=15$
따라서 답은 ②번입니다.

두 집합 $A=\left\{x~|~x는~12의~약수\right\}$, $B=\left\{x~|~x는~짝수\right\}$에 대하여 집합 $A\cap B$의 원소의 개수는? [2014.03/3점]
① $1$ ② $2$ ③ $3$ ④ $4$ ⑤ $5$
$A=\left\{x~|~x는~12의~약수\right\}=\left\{ 1,~2,~3,~4,~6,~12 \right\}$이죠. 이중에서 짝수만 고르면
2, 4, 6, 12
따라서 원소의 개수는 4이므로 답은 ④번입니다.
● 교환법칙, 결합법칙, 분배법칙
이제 처음 소개글에서 언급했던 것처럼 집합의 연산을 정의했으니 그 연산법칙을 알아볼 차례입니다. 우리가 중학교에서 유리수를 정의했을 때부터 알아봤던 기본 연산법칙에는 교환법칙, 결합법칙, 분배법칙이 있었죠. 자연스러운 원리인듯 보이면서도 이러한 법칙을 중요하게 짚고 가야하는 이유는 수학에는 엄청나게 다양한 연산들이 있으며 정의된 연산에 따라 이러한 법칙들이 성립하는 경우도 있지만 그렇지 않는 경우도 있기 때문입니다. 따라서 합집합과 교집합의 경우도 이러한 연산법칙이 성립하는지 확인해보는 과정은 필수죠.
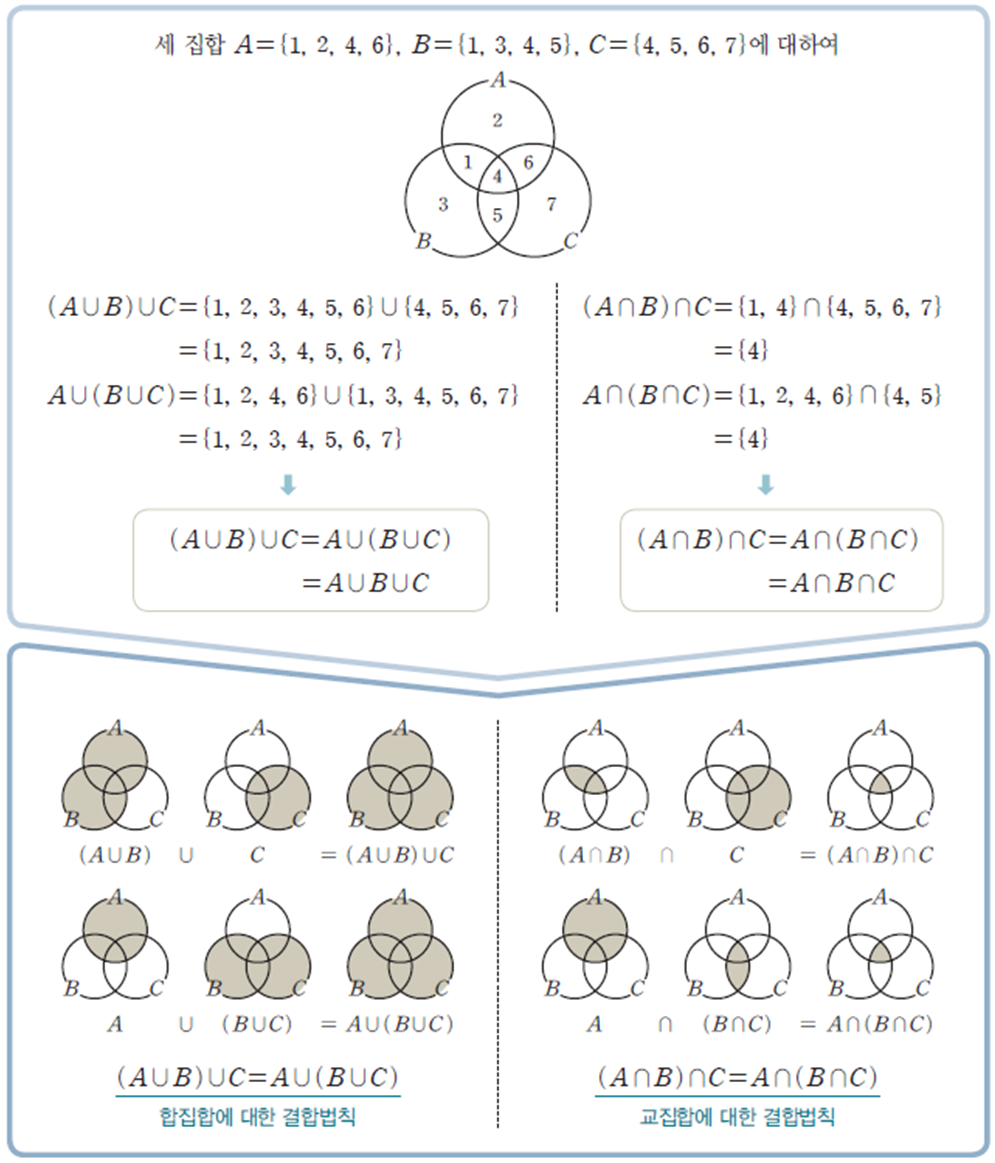
결론부터 얘기하면 합집합과 교집합은 교환법칙, 결합법칙, 분배법칙이 모두 통하는 착한 연산입니다. 그리고 고교 교육과정에서는 이에 대한 유도과정을 수학적 증명이 아니라 벤다이어그램을 통한 실험을 통해 직관적으로 이해하고 받아들이도록 하고 있습니다.
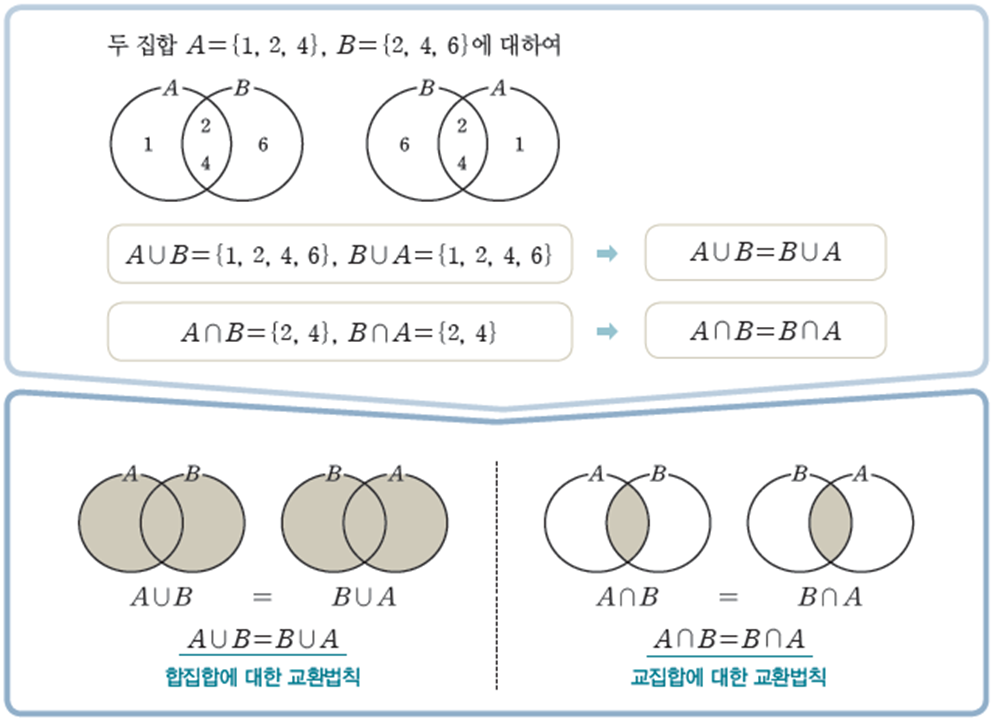
먼저 교환법칙(Commutative law)은 다음과 같이 연산하는 순서를 교환해도 결과가 같다는 원리입니다.
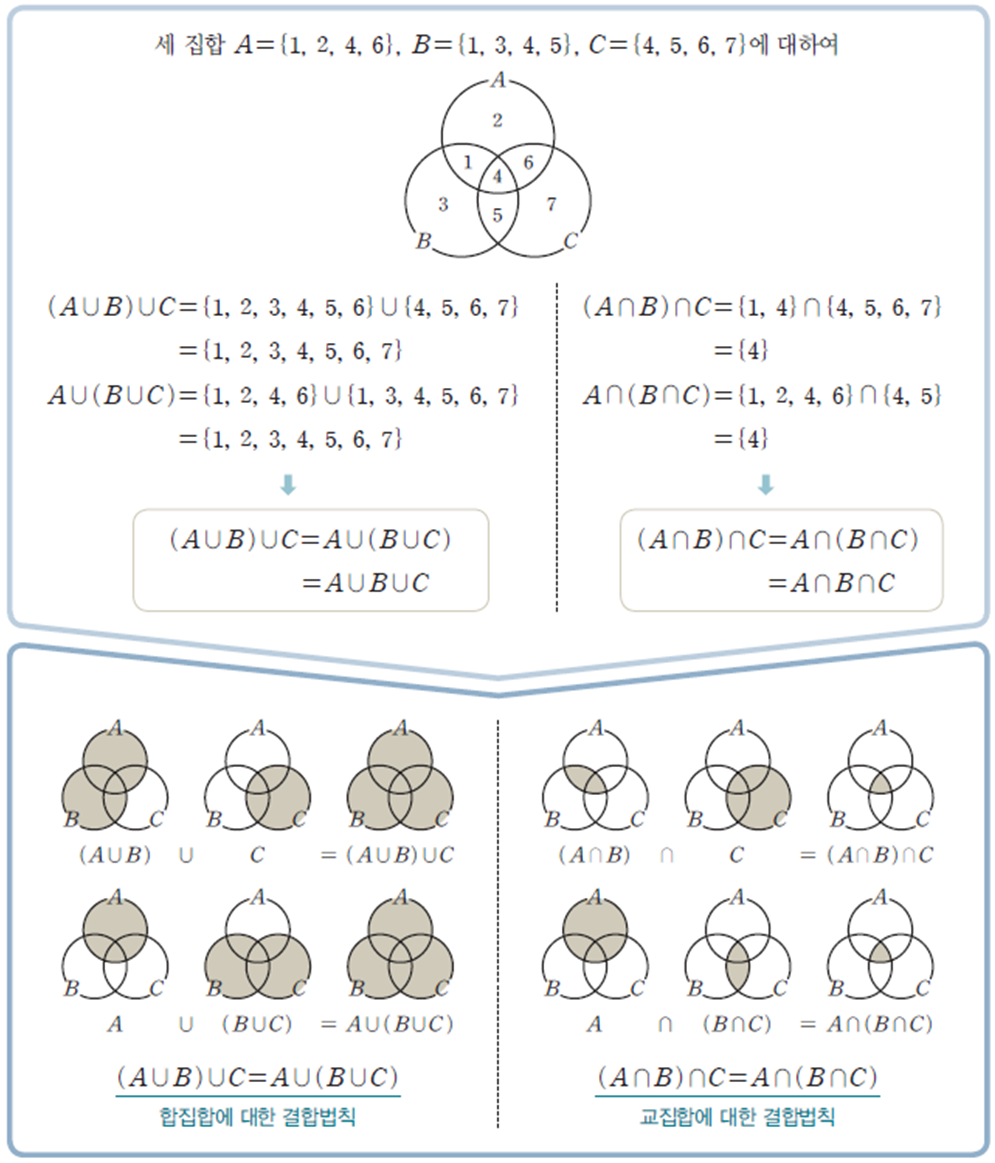
다음 결합법칙(Associative law)은 다음과 같이 괄호로 결합하는 방식에 상관없이 같은 결과를 낸다는 뜻입니다.
마지막으로 분배법칙(Distributive law)은 괄호 안과 괄호 밖의 연산이 다른 경우에 적용할 수 있습니다. 수의 연산에서 다음과 같이 곱셈과 덧셈에 대한 분배법칙을 알아본 적이 있죠. 여기에서 연산만 합집합과 교집합으로 바꿔주면 됩니다.
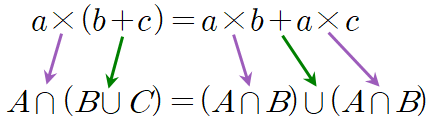
적용 예시와 함께 정리하면 다음과 같습니다.
수의 연산에서는 $a+(b\times c)=(a+b)\times(a+c)$와 같은 분배법칙은 성립하지 않지만 집합에서는 $A\cap(B\cup C)=(A\cap B)\cup (A\cap C)$와 $A\cup(B\cap C)=(A\cup B)\cap(A\cup C)$ 둘 다 성립하는 것도 특징입니다.
이상으로부터 다음과 같이 정리할 수 있습니다.

● 합집합, 교집합의 원소의 개수
집합에서는 원소의 중복을 허용하지 않기 때문에 두 집합 $A$, $B$에 대하여 $n(A)$, $n(B)$를 통해 합집합 $A\cup B$의 원소의 개수를 구해야 할 때는 중복계산이 일어나지 않도록 다음과 같이 교집합의 원소의 개수를 빼주면 됩니다.
$n(A\cup B)=n(A)+n(B)-n(A\cap B)$
이것은 벤다이어그램을 그려서 조금만 생각하면 금방 이해할 수 있는 공식이죠. 만약, 두 집합 $A$, $B$가 서로소라면 $n(A\cap B)=0$이므로 그냥 $n(A\cup B)=n(A)+n(B)$와 같이 구할 수 있죠.
또한, 양변에서 조금만 이항 하면 다음과 같이 교집합 $A\cap B$의 원소의 개수도 구할 수 있습니다.
$n(A\cap B)=n(A)+n(B)-n(A\cup B)$
예시와 함께 정리하면 다음과 같습니다.

추가적으로 앞에서 다음의 성질을 알아본 바 있죠.
$A\subset (A\cup B)$, $B\subset (A\cup B)$, $(A\cap B)\subset A$, $(A\cap B)\subset B$
부분집합의 원소의 개수는 원래 집합의 원소의 개수보다 많을 수 없으므로 다음이 성립합니다.
$n(A\cap B)\leq n(A)\leq n(A\cup B)$, $n(A\cap B)\leq n(B)\leq n(A\cup B)$

두 집합 $A$, $B$에 대하여 $n(A)=15$, $n(B)=11$, $n(A\cup B)=20$일 때, $n(A\cap B)$의 값을 구하시오.
$n(A\cap B)=n(A)+n(B)-n(A\cup B)$
$=15+11-20$=6
♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 집합과 명제' 카테고리의 다른 글
| 집합의 활용 - 수 체계의 집합 표현 및 포함 관계 (고1수학 집합과 명제) (6) | 2022.08.06 |
|---|---|
| 집합의 연산 - 드모르간의 법칙에 대한 쉽고 자세한 이해 (고1수학 집합과 명제) (0) | 2022.08.02 |
| 집합의 연산 - 여집합과 차집합의 기본 개념 이해 (고1수학 집합과 명제) (0) | 2022.07.31 |
| 집합 사이의 포함 관계 및 부분집합의 개념 이해 (고1수학 집합과 명제, 부분 집합의 개수 구하기) (1) | 2022.07.26 |
| 집합과 원소, 원소나열법, 조건제시법, 벤다이어그램의 개념 이해 (고1 수학 집합과 명제) (5) | 2022.07.24 |





댓글 영역