고정 헤더 영역
상세 컨텐츠
본문
절댓값 기호를 포함한 절대부등식 증명의 자세한 이해 (고1수학 집합과 명제, |a+b|≤|a|+|b|, |a|-|b|≤|a-b|)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
절대부등식의 두 번째 포스팅으로 이번 강의에서는 절댓값 기호를 포함한 절대부등식의 증명 방법에 대해 알아보겠습니다.

● 들어가기
지난 포스팅에서 언급했던 절대부등식 증명에 필요한 성질을 다시 확인해 보겠습니다.
| ■ 절대부등식에 자주 이용되는 성질 |
| $a$, $b$가 실수일 때 ① $a>b~\Leftrightarrow ~a-b>0$ ② $a^2\geq 0 $, $a^2+b^2\geq 0 $ ③ $|a|\geq 0$, $|a|\geq a$, $|a|^2=a^2$, $|ab|=|a| |b|$ ④ $a>0$, $b>0$일 때, $a>b\Leftrightarrow a^2>b^2$ |
위의 지난 포스팅에서는 ①, ②만 가지고 증명할 수 있는 절대부등식을 알아보았죠. 오늘 증명할 부등식에는 절댓값 기호가 들어가므로 ③번 성질이 사용되며, 절댓값으로 묶인 식은 그 자체를 뜯어볼 수 없고 제곱하면 없어지는 특징이 있으므로 ④번 성질 또한 함께 이용됩니다. 따라서 이전 강의에서 증명한 부등식보다는 그 과정이 다소 복잡하므로 어떤 아이디어와 절차로 부등식을 증명하는지 잘 참고하세요.
● |a+b|≤|a|+|b|의 증명
이 부등식의 증명은 어느 교과서에나 공통적으로 들어있는 예제 문제입니다. 절댓값 기호가 많이 붙어있는 변이 일반적으로 더 클 것이라 이해할 수 있겠죠? 이 부등식은 나중에 기하에서 벡터를 공부할 때도 일반화되는 공식으로서 삼각부등식이라고도 불리는데요. 왜 삼각부등식이라 불리는지는 그때 가서 이해할 수 있을 겁니다.
이 부등식의 증명에는 다음과 같이 ①, ③, ④번의 성질이 이용됩니다.

$a$, $b$가 실수일 때, 다음 부등식이 성립함을 증명하시오.
$|a|+|b|\geq |a+b|$
$|a+b|\geq 0$, $|a|+|b|\geq 0$이므로 다음이 성립함을 증명한다.
$(|a|+|b|)^2\geq |a+b|^2$
$(|a|+|b|)^2-|a+b|^2$
$=|a|^2+2|a||b|+|b|^2-(a+b)^2$
$=a^2+2|ab|+b^2-(a^2+2ab+b^2)$
$=2(|ab|-ab)$
이때, $|ab|\geq ab$이므로 $2(|ab|-ab)\geq 0$
따라서 $(|a|+|b|)^2\geq |a+b|^2$이므로 $|a|+|b|\geq |a+b|$이다.
이때, 등호는 $|ab|=ab$, 즉 $ab\geq 0$일 때 성립한다.
● |a|-|b|≤|a-b|의 증명
부등식 |a+b|≤|a|+|b| 만큼이나 자주 언급되는 부등식입니다. 우변에는 절댓값 기호가 전체에 씌어있지만 좌변은 개별적으로 씌어서 뺄셈으로 연결되어있으므로 음수가 될 수도 있죠. 따라서 일반적으로 우변이 더 크다고 이해할 수 있습니다.

$a$, $b$가 실수일 때, 다음 부등식이 성립함을 증명하시오.
$|a-b|\geq |a|-|b|$
예제1번과 마찬가지로 다음이 성립함을 먼저 보이겠습니다.
$|a-b|^2\geq (|a|-|b|)^2$
$|a-b|^2-(|a|-|b|)^2$
$=(a-b)^2-(|a|^2-2|a||b|+|b|^2)$
$=a^2-2ab+b^2-(a^2-2|ab|+b^2)$
$=2(|ab|-ab)\geq 0$
따라서 $|a-b|^2\geq (|a|-|b|)^2$가 성립하고 등호가 성립할 조건은 $|ab|=ab$, 즉 $ab\geq 0$입니다.
이제 제곱을 풀어서 원래 부등식을 증명해야 하는데 곧바로 $|a-b|\geq |a|-|b|$를 보이고 등호가 $ab\geq 0$일 때 성립한다고 하면 안 됩니다. 왜냐? $|a-b|\geq |a|-|b|$에서 $|a|-|b|$는 항상 0 이상이 아니기 때문이에요. 따라서 이 문제에서는 위의 ④번 성질인 '$a>0$, $b>0$일 때, $a>b\Leftrightarrow a^2>b^2$'를 적용하면 안 되는 거죠.
따라서 이 문제에서는 $|a|-|b|\geq 0$인 경우와 $|a|-|b|<0$인 경우로 나눕니다.
1) $|a|-|b|\geq 0$인 경우
$|a-b|\geq 0$이므로 $|a-b|^2\geq (|a|-|b|)^2$에서 ④번 성질을 통해 $|a-b|\geq |a|-|b|$가 되고 등호는 $ab\geq 0$일 때 성립합니다.
2) $|a|-|b|<0$인 경우
$|a|-|b|<0\leq |a-b|$이므로 $|a|-|b|< |a-b|$ 즉, 등호가 성립하지 않습니다.
1), 2)에 의해 $|a-b|\geq |a|-|b|$이고 등호는 $|a|-|b|\geq 0$인 경우에 한해서 $ab\geq 0$일 때 성립하므로, 등호가 성립할 조건은 $ab\geq 0$, $|a|\geq |b|$으로 정리할 수 있습니다.
위의 과정에서 유도한 부등식 $|a-b|^2\geq (|a|-|b|)^2$을 $|a-b|^2\geq \left|~|a|-|b|~ \right|^{~2}$로 바꿔서 생각해도 되겠죠? 제곱을 하면 어차피 똑같으니까요. 그런데 이렇게 보면 좌변의 $|a-b|$와 우변의 $\left|~|a|-|b|~ \right|$ 모두 0 이상이므로 이때는 ④번 성질을 바로 적용해서 다음을 유도할 수 있습니다.
$|a-b|\geq \left|~|a|-|b|~ \right|$
그리고 위의 예제처럼 $|a|-|b|\geq 0$인 경우와 $|a|-|b|<0$인 경우로 나눌 필요가 없으므로 등호가 성립할 조건은 $ab\geq 0$이 전부입니다.

$x$, $y$가 실수일 때, 다음 중 $|x-y|> \left|~|x|-|y|~ \right|$이기 위한 필요충분조건으로 옳은 것은?
① $xy<0$ ② $xy>0$ ③ $xy\geq 0$
④ $xy\leq 0$ ⑤ $x<0,~y<0$
일반적으로 부등식 $|x-y|\geq \left|~|x|-|y|~ \right|$이 성립하고 등호가 성립할 조건이 $xy\geq 0$입니다. 이 말은 $xy\geq 0$이 아닌 경우, 즉 $xy<0$인 경우에는 등호가 성립하지 않고 $|x-y|> \left|~|x|-|y|~ \right|$만 성립합니다.
따라서 답은 ①번입니다.
● |a+b|≤|a|+|b|의 활용
예제1에서 증명했던 부등식 $|a|+|b|\geq |a+b|$을 이미 알고 있다고 가정하면 이 식에다가 $a$ 대신 $a-b$를 대입하면 다음과 같이 예제2의 부등식을 바로 유도할 수 있습니다.
$|{\color{Red}a-b }|+|b|\geq |{\color{Red}a-b }+b|$
$\Rightarrow |a-b|+|b|\geq |a|$
$\Rightarrow |a-b|\geq |a|-|b|$
그리고 $|a|+|b|\geq |a+b|$에서 등호가 성립할 조건은 $ab\geq 0$이므로 여기에도 $a$ 대신 $a-b$를 대입하면 $|a-b|\geq |a|-|b|$의 등호 성립 조건은 $({\color{Red}a-b })b\geq 0$ 즉, $ab\geq b^2$입니다. 위의 예제에서 유도한 등호가 성립할 조건인 $ab\geq 0$, $|a|\geq |b|$와는 좀 달라 보일 텐데요. 아래 접은 글을 펼쳐보시면 둘의 관계는 필요충분조건임을 알 수 있습니다.
1) $ab\geq 0$, $|a|\geq |b|$일 경우
$|a|\geq |b|\Rightarrow |ab|\geq |b|^2$
$ab\geq 0$ 즉, $|ab|=ab$이므로
$|ab|\geq |b|^2\Rightarrow$ $ab\geq b^2$
2) $ab\geq b^2$일 경우
$ab\geq b^2$ $\geq 0$이므로 $ab=|ab|=|a||b|$이다. 따라서
$ab\geq b^2\Rightarrow |a||b|\geq |b|^2$
$\Rightarrow$ $|a|\geq |b|$
1), 2)에 의해 $ab\geq 0$, $|a|\geq |b|$와 $ab\geq b^2$는 필요충분조건이다.

$x$, $y$가 실수일 때, 다음 중 $|x|+|y|= |x-y|$이기 위한 필요충분조건인 것은?
① $xy<0$ ② $xy>0$ ③ $xy\geq 0$
④ $xy\leq 0$ ⑤ $x<0,~y<0$
부등식 $|x|+|y|\geq |x+y|$에서 $y$를 $-y$로 바꾸면 다음과 같이 문제의 부등식이 유도됩니다.
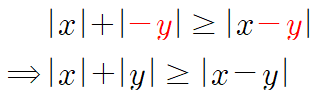
따라서 등호가 성립할 조건 역시 $|x|+|y|\geq |x+y|$의 조건 $xy\geq 0$에서 $y$를 $-y$로 바꾸면
$x({\color{Red}-y})\geq 0 \Rightarrow xy\leq 0$
따라서 답은 ④번입니다.
♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 집합과 명제' 카테고리의 다른 글
| 산술평균, 기하평균 부등식의 활용 - 최대, 최소 구하기 (고1수학 집합과 명제, 절대부등식) (4) | 2022.09.06 |
|---|---|
| 산술평균, 기하평균, 조화평균의 개념 이해 (고1수학 집합과 명제, 절대부등식) (2) | 2022.08.31 |
| 절대부등식의 개념 및 기본 증명의 자세한 이해 (고1수학 집합과 명제) (6) | 2022.08.29 |
| 여러 가지 논리 문제에 대한 남다른 해설 (고1수학 집합과 명제, 논리력 테스트) (1) | 2022.08.26 |
| 충분조건과 필요조건에 대한 자세한 이해 (고1수학 집합과 명제) (4) | 2022.08.25 |





댓글 영역