고정 헤더 영역
상세 컨텐츠
본문
절대부등식의 개념 및 기본 증명의 자세한 이해 (고1수학 집합과 명제)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
이제 명제 단원에서 절대부등식 파트만 남았습니다. 절대부등식은 부등식을 다루는 내용이라 앞부분 방정식과 부등식의 연장으로 볼 수도 있어요. 그러나 이 내용이 명제 단원에 속하게 된 이유는 주된 내용이 증명으로 시작하기 때문입니다. 오늘부터는 절대부등식에 대한 내용으로 강의를 시작하겠습니다.

● 절대부등식의 뜻
절대부등식은 절대적으로 성립하는 부등식으로 전체집합에 속한 모든 값에 대하여 성립하는 부등식을 의미합니다. 한편, 항상 성립하는 등식은 '항등식'이라고 배운 적이 있었죠. 즉, 절대부등식은 항등식의 정의에서 '등식'만 '부등식'으로 바꾼 개념이라 생각할 수 있습니다. 그래서 절대부등식을 '항부등식'이라고 부르기도 합니다.
예를 들어 $x^2\geq 4$, $x^2\geq 0$ 등은 모두 부등식이죠. 이 중에서 부등식 $x^2\geq 0$은 모든 실수 $x$에 대하여 성립하므로 절대부등식이 됩니다.
한편, $ax+b\geq 0$과 같은 일차부등식의 경우 $y=ax+b$의 그래프를 그리면 항상 $x$과 만나므로 그 점의 좌표를 경계로 하여 한쪽은 부등식의 해가 되고 다른 쪽은 해가 되지 않죠. 따라서 일차부등식에서는 절대부등식이 존재하지 않습니다.
즉, 이 절대부등식 파트에서 다루는 문제들은 대부분이 이차부등식이라는 점도 참고해 두세요.
● 절대부등식의 증명
절대부등식을 증명할 때는 다음과 같은 성질이 자주 이용됩니다.
| ■ 절대부등식에 자주 이용되는 성질 |
| $a$, $b$가 실수일 때 ① $a>b~\Leftrightarrow ~a-b>0$ ② $a^2\geq 0 $, $a^2+b^2\geq 0 $ ③ $|a|\geq 0$, $|a|\geq a$, $|a|^2=a^2$, $|ab|=|a| |b|$ ④ $a>0$, $b>0$일 때, $a>b\Leftrightarrow a^2>b^2$ |
위의 성질들은 이미 알고 있는 것이므로 따로 보충 설명을 할 필요는 없겠죠. 이중에서도 가장 기본적으로 사용되는 성질이 ①, ②번입니다. 기본적인 부등식의 증명은 우변을 0으로 만들고 좌변을 완전제곱꼴로 만드는 방식을 따릅니다.

$a$, $b$가 실수일 때, 부등식 $a^2+b^2\geq ab$이 성립함을 증명하시오.
주어진 부등식의 우변을 좌변으로 이항한 다음 부등식을 증명하면 된다.
$a^2-ab+b^2\geq 0$
위의 식에서 좌변을 완전제곱꼴로 변형하면
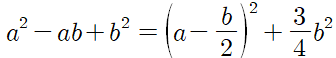
$a$, $b$가 실수이므로
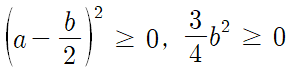
따라서 $a^2-ab+b^2\geq 0$이 성립하므로 $a^2+b^2\geq ab$이 성립한다.
이때, 등호는 $a-\frac{b}{2}=0$, $\frac{3}{4}b^2=0$, 즉, $a=b=0$일 때 성립한다.
여기서 유의해야 할 점은 등호를 포함한 부등식을 증명할 때는 반드시 등호가 성립하는 조건을 구해줘야 한다는 점입니다. 만약, 등호가 성립할 조건이 언급되지 않는다면 부등식에서 $\geq $인지 $>$인지 확실하지 않기 때문입니다. 따라서 어느 교과서든 다음과 같은 유의사항이 언급되어 있습니다.


$a$, $b$가 실수일 때, 부등식 $a^2+b^2+c^2\geq ab+bc+ca$가 성립함을 증명하시오.
예제1번에서 한 단계 확장된 부등식입니다. 이 식 또한 같은 원리로 증명할 수 있으며 다항식에서 곱셈 공식을 공부할 때 한 번쯤은 본 적이 있었을 겁니다. 증명 과정은 다음과 같습니다.
주어진 부등식의 우변을 좌변으로 이항한 다음 부등식을 증명하면 된다.
$a^2+b^2+c^2-ab-bc-ca\geq 0$
위의 식의 좌변에 2를 곱하면
$2a^2+2b^2+2c^2-2ab-2bc-2ca$
좌변을 서로 다른 문자끼리 묶어 완전제곱식을 만들면
$(a-b)^2+(b-c)^2+(c-a)^2$
$(a-b)^2\geq 0$, $(b-c)^2\geq 0$, $(c-a)^2\geq 0$이므로
$2a^2+2b^2+2c^2-2ab-2bc-2ca$
$=(a-b)^2+(b-c)^2+(c-a)^2\geq 0$
따라서 $a^2+b^2+c^2-ab-bc-ca\geq 0$이므로 $a^2+b^2+c^2\geq ab+bc+ca$가 성립한다.
이때, 등호는 $a-b=b-c=c-a=0$, 즉, $a=b=c$일 때 성립한다.

$a>0$, $b>0$일 때, 다음 부등식이 성립함을 증명하시오. [미래엔 수학]
$a^3+b^3\geq ab(a+b)$
$a^3+b^3-ab(a+b)$
$=(a+b)(a^2-ab+b^2)-ab(a+b)$
$=(a+b)\left\{(a^2-ab+b^2)-ab \right\}$
$=(a+b)(a^2-2ab+b^2)$
$=(a+b)(a-b)^2$
$a+b>0$이고 $(a-b)^2\geq 0$이므로 $(a+b)(a-b)^2\geq 0$이다.
따라서 $a^3+b^3\geq ab(a+b)$이고 등호는 $a=b$일 때 성립한다.
교과서의 문제 중에선 꽤나 어려운 증명에 속하지만 앞에서 필요한 설명은 다 했으므로 자잘한 설명 없이 꼭 필요한 골자만 적었습니다. 실제로도 내신 시험에서 이런 문제가 서술형으로 등장하면 장황한 설명을 구구절절 쓸 시간이 부족하죠. 따라서 제가 위해서 언급한 내용만 빠뜨리지 않고 잘 작성하면 만점을 받을 수 있습니다.

● 오개념 잡기
수업 시간에 예제3번을 학생에게 시켜보면 다음과 같이 푸는 경우가 있습니다.
| $a^3+b^3\geq ab(a+b)$ $(a+b)(a^2-ab+b^2)\geq ab(a+b)$ $a^2-ab+b^2\geq ab~~(\because a+b>0)$ $a^2-2ab+b^2\geq 0$ $(a-b)^2\geq 0$ 따라서 부등식은 참이고 등호는 $a=b$일 때 성립한다. |
이렇게 풀면 몇 점이나 받을 수 있을까요? 채점을 까다롭게 하시는 선생님을 잘못 만난다면 1점도 채 못 받을 수도 있어요. 왜 그럴까요? 논리적 순서가 잘못됐기 때문입니다. 보여야 하는 식이 가장 먼저 등장하고 그 식을 분석해서 $(a-b)^2\geq 0$라는 결과에 도달했으므로 $a^3+b^3\geq ab(a+b)$임을 이용해서 $(a-b)^2\geq 0$임을 증명한 것이죠.
차라리 다음과 같이 기호 '$\Leftrightarrow $'을 추가하고 마지막에 결론을 추가하면 온전한 증명이 될 수 있습니다.
| $a^3+b^3\geq ab(a+b)$ $\Leftrightarrow (a+b)(a^2-ab+b^2)\geq ab(a+b)$ $\Leftrightarrow a^2-ab+b^2\geq ab~~(\because a+b>0)$ $\Leftrightarrow a^2-2ab+b^2\geq 0$ $\Leftrightarrow (a-b)^2\geq 0$ 따라서 $(a-b)^2\geq 0$로부터 $a^3+b^3\geq ab(a+b)$가 성립하고 등호는 $a=b$일 때 성립한다. |
단, 전에도 언급했듯이 필요충분조건의 기호를 쓸 때는 양쪽 방향이 다 성립해야 하므로 주의할 필요가 있어요. 따라서 기호 '$\Rightarrow $'만 사용해서 전개할 때는 다음과 같이 대우법을 쓰는 것도 방법이 될 수 있습니다.
| $a^3+b^3< ab(a+b)$ $\Rightarrow (a+b)(a^2-ab+b^2)< ab(a+b)$ $\Rightarrow a^2-ab+b^2< ab~~(\because a+b>0)$ $\Rightarrow a^2-2ab+b^2< 0$ $\Rightarrow (a-b)^2< 0$ 따라서 $a^3+b^3< ab(a+b) \Rightarrow(a-b)^2< 0$이 참이므로 $(a-b)^2\geq 0$로부터 $a^3+b^3\geq ab(a+b)$가 성립하고 등호는 $a=b$일 때 성립한다. |
♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 집합과 명제' 카테고리의 다른 글
| 산술평균, 기하평균, 조화평균의 개념 이해 (고1수학 집합과 명제, 절대부등식) (2) | 2022.08.31 |
|---|---|
| 절댓값 기호를 포함한 절대부등식 증명의 자세한 이해 (고1수학 집합과 명제) (2) | 2022.08.30 |
| 여러 가지 논리 문제에 대한 남다른 해설 (고1수학 집합과 명제, 논리력 테스트) (1) | 2022.08.26 |
| 충분조건과 필요조건에 대한 자세한 이해 (고1수학 집합과 명제) (6) | 2022.08.25 |
| 귀류법에 대한 이해, 귀류법과 대우법의 차이 (고1수학 집합과 명제) (7) | 2022.08.24 |





댓글 영역