고정 헤더 영역
상세 컨텐츠
본문
절대부등식을 활용한 최대, 최소 구하는 초고난도 문제 풀이 (고1 수학 명제 심화)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽게 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
고1 수학에서 명제를 공부하면 맨 뒤에 절대부등식을 만나게 되는데 학원이나 사설 문제집으로 공부해 보면 다른 단원보다 유독 문제 유형이 많이 수록된 단원이 절대부등식입니다. 특히, 절대부등식을 활용하여 최댓값이나 최솟값을 구하는 유형이 많죠. 오늘은 절대부등식을 활용하여 해결할 수 있는 고난도 문제를 몇 개 풀어보도록 하겠습니다.

이 글에서 다루는 유형은 수능이나 모의고사에는 전혀 등장하지 않습니다. 교과서에서도 절대부등식의 내용 자체가 많지 않고, 간단한 증명과 산술-기하 부등식을 간단히 활용하는 수준에서만 다루기 때문에 교과서의 수준과도 많이 동떨어진 문제라 내신시험에서도 출제하기에 적절하다고 볼 수는 없습니다. 하지만 1등급 학생들을 가려내야 하는 선생님 입장에서 수단과 방법을 가리지 않는다면 어떻게 출제하실지는 알 수 없으므로 1등급을 목표로 하는 학생들은 참고 삼아 공부해 보시기 바랍니다.

양수 $x$, $y$, $z$에 대하여 다음 식의 최솟값을 구하시오.
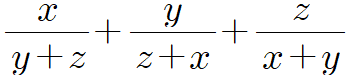
$x$를 엄청 큰 양수로 놓고 $y$, $z$를 0에 가까운 양수로 놓으면 주어진 식은 얼마든지 크게 만들 수 있으므로 최댓값은 없을 거라 짐작할 수 있겠죠. 그럼 어떻게 해야 최솟값이 나올 것인가? 직감으로 예상하면 세 양수가 같은 값을 가질 경우 $\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=\frac{3}{2}$이 될 거라 짐작할 수는 있습니다.
이제 이 식을 어떻게 변형해야 할지 알아보겠습니다. $x$, $y$, $z$가 삼대칭을 이루는 형태라 보통 이런 상황에서는 세 양수의 곱이나 합을 생각해 볼 수 있어요. 여기서는 $x+y+z=S$로 놓고 생각해 보겠습니다. 그리고 각 식에의 분자를 변형하면 다음과 같습니다.
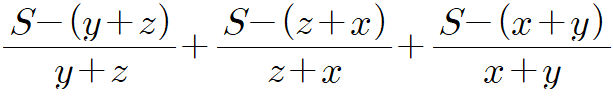
그럼 이 식에서 분자에 $S$만 남기고 정리하면
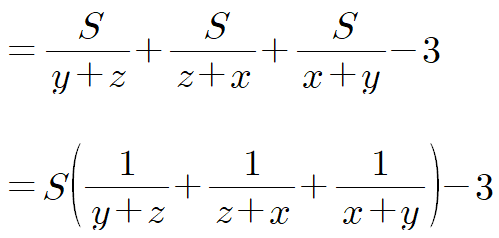
여기서 중요한 스킬이 사용되는데 각 분모인 $y+z$, $z+x$, $x+y$들을 각각 $a$, $b$, $c$로 치환하면
$a+b+c=(y+z)+(z+x)+(x+y)$
$=2(x+y+z)=2S$
임을 알 수 있어요. 즉, $S=\frac{1}{2}(a+b+c)$이므로 본 식은 다음과 같이 나타낼 수 있습니다.
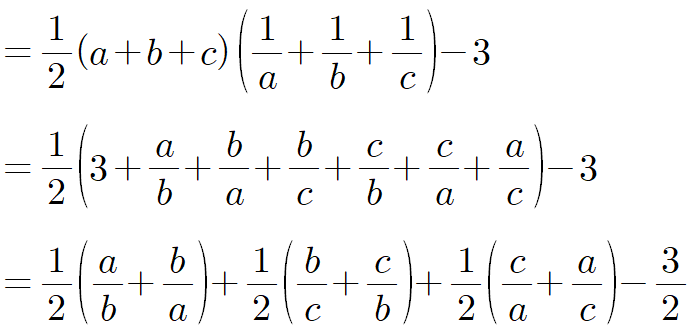
여기까지 오는 게 무지 어렵죠. $x$, $y$, $z$는 모두 양수이므로 $y+z$, $z+x$, $x+y$를 각각 치환한 $a$, $b$, $c$도 모두 양수입니다. 그럼 이제 여기서 뭘 쓰면 될지는 아시겠죠? 괄호로 묶은 각 식에다가 산술-기하 부등식을 동시에 적용합니다. 우선 앞의 식부터 해보면
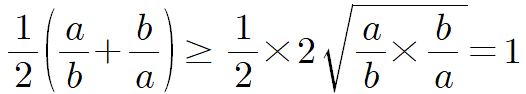
이고 등호는 $\frac{a}{b}=\frac{b}{a}$ 즉, $a=b$일 때, 성립합니다. 따라서 이 식의 최솟값은 $1$이 됩니다.
같은 방법으로 나머지 식들도 전부 최솟값은 $1$이고 이 경우 $b=c$, $c=a$임을 알 수 있어요.
따라서 본식의 최솟값은 $1+1+1-\frac{3}{2}=$ $\frac{3}{2}$이 되고 이 경우 $a=b=c$입니다.
즉, $x+y=y+z=z+x$이므로 $x=y=z$인 경우가 됩니다.

양수 $a$, $b$, $c$에 대하여 $a+b+c=1$일 때, 다음식의 최댓값을 구하시오.
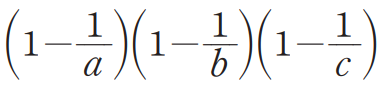
이 식을 마냥 통분해서 정리하면 답이 보이지 않습니다. 다만, $a$, $b$, $c$가 모두 같은 값을 가지면 최댓값이 되지 않을까 짐작해 볼 수는 있죠. 이 문제 역시 어떻게 변형해서 처리하느냐가 관건인데 우선 괄호로 묶인 식들을 각각 통분해 보면
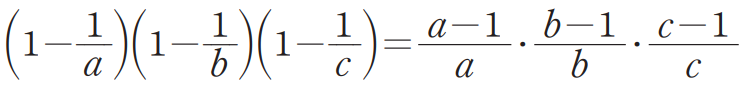
그리고 여기서 $a+b+c=1$라는 조건으로부터 다음의 관계식을 이용합니다.
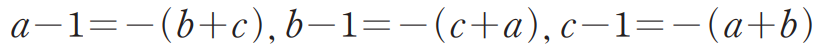
그럼 정리한 식은 다음과 같이 변형할 수 있어요.
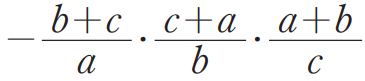
여기까진 할 수 있다 해도 그다음을 어떻게 해야 할지가 막막할 텐데 여기서부터 $a$, $b$, $c$가 모두 양수임을 이용하여 분자의 각 식 $b+c$, $c+a$, $a+b$에다가 다음과 같이 산술-기하 부등식을 적용합니다.
$b+c\geq 2\sqrt{bc}$
$c+a\geq 2\sqrt{ca}$
$a+b\geq 2\sqrt{ab}$
위의 3개의 부등식은 $a=b=c$일 때 등호가 동시에 성립하죠. 이 사실로부터 다음의 부등식을 유도할 수 있습니다.
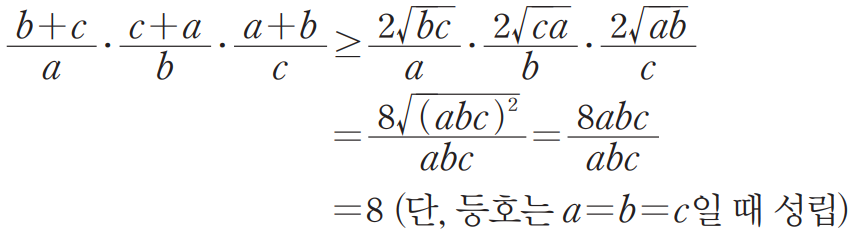
이렇게 만들어진 3개의 루트식을 정리하면 $a$, $b$, $c$가 하나씩 튀어나오기 때문에 분모의 $abc$와 약분이 되는 놀라운 일이 벌어지죠. 따라서 이 식은 $a=b=c$일 때 정확하게 $8$이 됩니다.
이제 우리가 최솟값을 원했던 식은 위의 식에 마이너스가 붙어있었으므로 구하는 최솟값은 $-8$이 됩니다.

양수 $a$, $b$에 대하여 다음식의 최솟값을 $m$이라 하고 이때의 $a$, $b$의 값을 각각 $p$, $q$라 할 때, $mpq$의 값을 구하시오.
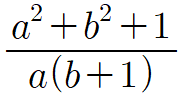
콴다 앱으로 검색하면 판별식이나 미분을 이용한 풀이는 있어도 절대부등식을 이용한 풀이는 검색되지 않는 문제입니다. 그런데 판별식을 이용한 최대, 최소는 고등학교 교육과정에는 아예 존재하지 않는 개념이므로 여기서는 다루지 않겠습니다. 이 문제에서는 산술-기하 부등식과 코시-슈바르츠 부등식이 필요합니다.
양변을 $a^2$으로 나누면
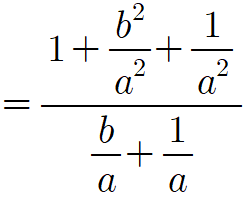
여기서 $\frac{b}{a}=x$, $\frac{1}{a}=y$로 치환하면
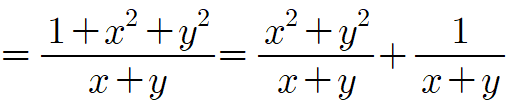
여기서 다음과 같은 코시-슈바르츠 부등식을 이용합니다.
$(1^2+1^2)(x^2+y^2)\geq (x+y)^2$
(등호는 $x=y$일 때, 성립)
따라서 위의 식을 다음과 같이 바꾸고 부등식을 적용하면
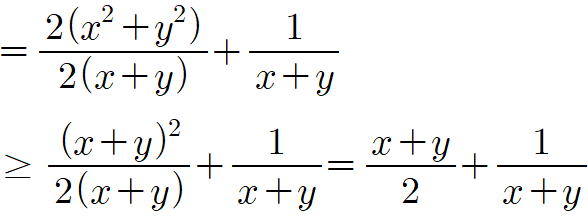
이제 $a$, $b$가 양수이므로 이들로 이루어진 식을 치환한 $x$, $y$도 각각 양수이고 따라서 $x+y$도 양수이므로 여기서 산술-기하 부등식을 적용할 수 있어요.
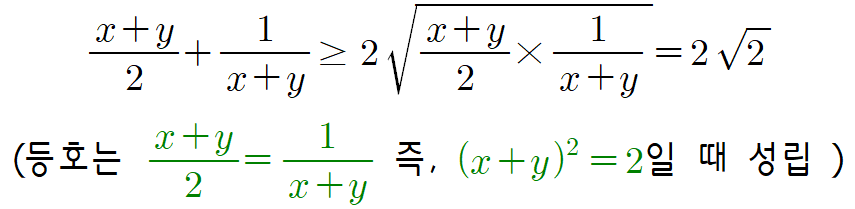
이 과정으로부터 문제의 식이 $2\sqrt{2}$보다 같거나 크다는 것을 알 수 있는데 이제부터 중요한건 이 식이 과연 $2\sqrt{2}$와 같아질 수 있는가겠죠. 그러기 위해서는 적용한 두 가지 부등식에서 등호가 동시에 성립할 수 있어야 합니다.
즉, 위에서 알아본 등호 성립 조건인 $x=y$와 $(x+y)^2=2$가 동시에 성립하면 됩니다. 따라서 둘을 연립하면 $(2x)^2=2$이고 $2x$는 양수이므로 $2x=\sqrt{2}$이죠. 따라서 등호가 성립하는 순간의 $x$, $y$의 값은
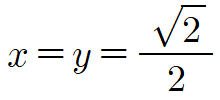
따라서 본식의 최솟값은 $2\sqrt{2}$이므로 $m=2\sqrt{2}$입니다. 이제 치환을 풀어서 $a$, $b$의 값까지 구하면
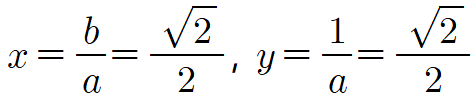
$a=\sqrt{2},~b=1$
따라서 $p=\sqrt{2}$, $q=1$입니다.
이상으로부터 $mpq=2\sqrt{2}\times \sqrt{2}\times 1=$ $~4~$입니다.
♥ 이해가 잘 되셨다면 좋아요와 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 집합과 명제' 카테고리의 다른 글
| '모든', '어떤'이 있는 명제의 가정, 결론, 역, 대우에 대한 자세한 이해 (고1 수학 집합과 명제 심화) (0) | 2023.09.26 |
|---|---|
| 코시-슈바르츠 부등식에 대한 자세한 이해 (고1수학 집합과 명제, 절대부등식) (6) | 2022.09.07 |
| 산술평균, 기하평균 부등식의 활용 - 최대, 최소 구하기 (고1수학 집합과 명제, 절대부등식) (4) | 2022.09.06 |
| 산술평균, 기하평균, 조화평균의 개념 이해 (고1수학 집합과 명제, 절대부등식) (2) | 2022.08.31 |
| 절댓값 기호를 포함한 절대부등식 증명의 자세한 이해 (고1수학 집합과 명제) (2) | 2022.08.30 |





댓글 영역