고정 헤더 영역
상세 컨텐츠
본문
인수정리를 이용한 인수분해에 대한 자세한 이해 (고1수학 다항식)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
계속해서 인수분해에 대한 포스팅을 이어가겠습니다. 오늘은 인수정리에 대해 알아보겠습니다. 일반적인 삼차식이나 사차식을 인수분해할 때 인수정리를 이용할 수 있는데 이런 방법이 방정식 풀이에도 그대로 이용되기 때문에 인수정리는 인수분해를 위한 가장 핵심 원리라고 볼 수 있습니다.

● 인수정리
서두에서 소개했듯이 인수정리는 나머지정리로부터 유도되는 정리이며 나머지가 특정한 값을 가질 때의 개념이므로 나머지정리의 특수한 경우라고 볼 수 있습니다.

나머지정리에 의해 $P(x)$를 일차식 $x-\alpha $로 나눈 나머지가 $P(\alpha )$이므로 특별한 유도과정 없이 위의 정리는 자명합니다. $x-\alpha $로 나누어 떨어진다는 것은 $P(x)$는 $x-\alpha $를 인수로 가진다는 뜻이므로 인수정리라고 부릅니다.
위의 정리를 일반적인 일차식 $ax+b$로 설명하면 다음과 같습니다.

예를 들어, 이전 포스팅에서 다음의 계산에 의해 $2x ^{3} +3x ^{2} -x-1$을 $2x+1$로 나눈 나머지가 $0$임을 알아본바 있습니다.
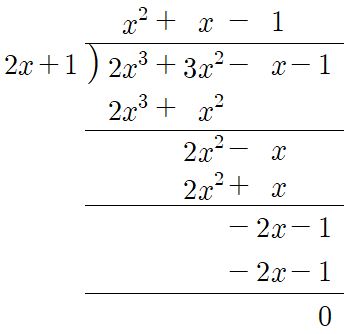
이제 이 식에다가 일차식 $2x+1$의 값이 $0$이 되는 $x=-\frac{1}{2}$을 대입해 보면
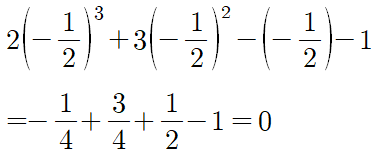
이므로 직접 계산 없이도 인수정리에 의해 $2x ^{3} +3x ^{2} -x-1$이 $2x+1$로 나누어 떨어짐을 알 수 있습니다.

$x$에 대한 다항식 $2x ^{3} +ax ^{2} +bx+6$이 $x^2-1$로 나누어 떨어질 때, $ab$의 값은? (단, $a$, $b$는 상수이다.) [2014.06.교육청/3점]
① $6$ ② $8$ ③ $10$ ④ $12$ ⑤ $14$
$x^2-1=(x-1)(x+1)$이므로 주어진 다항식은 $x-1$로도 나누어 떨어지고 $x+1$로도 나누어 떨어집니다. 여기서 이용되는 개념이 바로 인수정리죠.
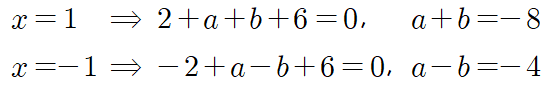
연립방정식을 풀면 $a=-6$, $b=-2$입니다. 따라서 $ab=12$이므로 답은 ④번입니다.
● 인수정리를 이용한 인수분해
삼차식 $x^3-7x+6$은 어떻게 인수분해를 해야 할까요? 앞에서 공부했던 공식을 써먹을 수 있는 것도 아니면서 치환할 모양새가 보이지도 않습니다. 이런 다항식을 인수분해할 때 바로 인수정리가 활용됩니다.
위의 다항식을 $P(x)$라 하면 $P(1)=0$이 성립하죠? 그럼 인수정리에 의해 $P(x)=x^3-7x+6$은 $x-1$로 나누어 떨어진다는 것을 알 수 있습니다. 그럼 이제 남은 계산은 어떻게 하면 될까요? 직접 나눗셈을 해도 되지만 일차식으로 나누는 것이므로 이전에 공부했던 조립제법을 여기서 써먹으면 더 좋겠죠~!
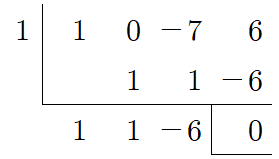
위와 같이 조립제법으로 계산할 수 있어요. 나누어 떨어진다는 사실을 알고 있으므로 나머지가 $0$이 되는지 확인해 줄 필요도 있고요. 계산 결과에 의해
$x^3-7x+6=(x-1)(x^2+x-6)$
여기서 $x^2+x-6$도 인수분해가 되므로 최종 결과는
$x^3-7x+6=(x-1)(x-2)(x+3)$
● 인수정리에서 $\alpha $ 찾기
서두에서도 얘기했듯이 위와 같은 인수분해는 뒤에서 방정식의 해를 구할 때 자주 이용되므로 모든 인수분해 전략 중에 가장 중요하다고 볼 수 있습니다. 그럼 인수정리를 활용하기 위해 핵심적으로 체크해야 할 부분이 있죠. 맨 처음에 했던 $P(\alpha )=0$을 만족하는 $\alpha $를 찾아주는 것입니다. 이것만 찾으면 조립제법으로 계산만 해주면 되니까요. 단, 그런 $\alpha $를 어떻게 찾아내느냐가 문제가 됩니다. 위에서 해본 예시처럼 $\alpha =1$이 딱 보이는 다항식이라면 쉽지만 조금만 숫자를 바꿔도 상당히 어려워질 수도 있죠. 위의 예시를 다시 보면서 이런 $\alpha $의 특징을 알아보도록 하겠습니다.
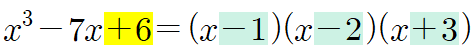
좌변에서 최고차항의 계수가 1이기 때문에 우변에서 분해된 모든 일차식의 일차항 계수도 1임을 알 수 있습니다. 따라서 위의 식에서 파란색으로 표시한 각 일차식의 상수에서 $(-)$부호를 붙인 값이 바로 $\alpha $가 됩니다. 위의 인수분해 과정에서 $\alpha $가 가질 값으로 $1$을 찾았지만 $2$나 $-3$도 $\alpha $가 될 수 있었다는 거죠. 그리고 계수비교법에 의해 이들의 상수를 모두 곱한 값이 좌변의 노란색으로 표시한 상수와 같습니다. 즉, 양쪽 식을 비교하면
$+6$ $=$ $(-1)\times (-2)\times (3)$
이죠. 결국 $\alpha $는 본 식의 상수인 $6$의 약수 중에서 부호를 적절히 붙여서 찾을 수 있다는 사실을 알 수 있습니다.

다항식 $2x ^{4} -2x ^{3} -3x ^{2} -x-2$을 계수가 정수인 범위에서 인수분해 하시오..
앞에서 정리한 내용에 의하면 위의 식을 $P(x)$라 했을 때, $P(x)$의 상수는 $-2$이고 $2$의 약수는 $1$, $2$이므로 $P(\alpha )=0$을 만족하는 $\alpha $는 $\pm 1$, $\pm 2$중에 존재합니다. 이 중에서 하나씩 대입하여 0이 되는 값을 찾습니다. 이때
$P(-1)=2+2-3+1-2=0$
이므로 $\alpha =-1$로 놓고 인수정리를 이용할 수 있죠. 이제 다음과 같이 조립제법으로 나눗셈을 해줍니다.
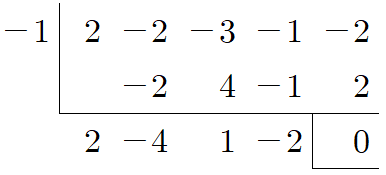
$2x ^{4} -2x ^{3} -3x ^{2} -x-2=(x+1) (2x ^{3} -4x ^{2} +x-2)$
이렇게 해서 삼차식의 몫이 나옵니다. 이걸 또 인수분해 하려면 인수정리를 한 번 더 이용해야 하죠.
이제 $x=2$를 대입해 보면 $2\times 2 ^{3} -4\times 2 ^{2} +2-2=0$이 되어 $2$로 조립제법을 또 쓸 수 있어요. 만약 처음 주어진 사차식에서 $-1$과 $2$를 모두 찾았다면 다음과 같이 조립제법을 연달아 이용할 수도 있습니다.

따라서 답은
$2x ^{4} -2x ^{3} -3x ^{2} -x-2=$ $( x+1)( x-2) (2x ^{2} +1)$

다항식 $a^5-b^5$을 계수가 정수인 범위에서 인수분해 하시오.
$a^3-b^3$이 $(a-b)(a^2+ab+b^2)$로 인수분해가 된다는 사실은 이미 알고 있죠. 이 문제는 $a^n-b^n$ 형태의 인수분해가 어떻게 이루어지는지를 암시해 줍니다.
주어진 문자 그대로 인수분해를 할 수도 있지만 이해를 돕기 위해 편의상 $a=x$로 바꿔서 $x^5-b^5$을 인수분해하는 문제로 생각해 봅시다. 여기서 $x$는 변수, $b$는 상수처럼 생각하는 거죠.
이 식을 $0$으로 만들 수 있는 $x$의 값은 $x=b$임을 금방 알 수 있으므로 다음과 같이 조립제법으로 나눗셈을 합니다.
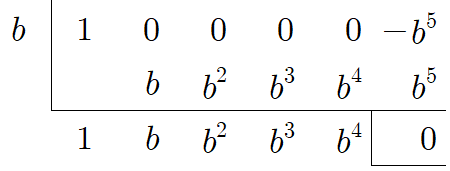
$x ^{5} -b ^{5} =(x-b)(x ^{4} +bx ^{3} +b ^{2} x ^{2} +b ^{3} x+b ^{4} )$
이제 다시 $x=a$를 대입하면
$(a-b)(a ^{4} +a ^{3} b+a ^{2} b ^{2} +ab ^{3} +b ^{4} )$
예제3과 같은 인수분해는 나중에 수학Ⅱ에서 다항함수의 미분 공식을 유도할 때 활용됩니다.
● $\alpha $가 정수가 아닌 경우 (심화)
인수정리를 이용할 때 $\alpha $가 정수가 아닌 유리수라면 고려해야 할 것이 하나 더 생깁니다. 예를 들어 다음 다항식은 어떻게 인수분해될까요?
$24x^3+26x^2+9x+1$
이 다항식은 상수가 $1$인데 $x=\pm 1$일 때는 위의 식이 $0$이 되지 않죠. 결과부터 보여드리면 이 다항식은 다음과 같이 인수분해됩니다.
$24x^3+26x^2+9x+1=(2x+1)(3x+1)(4x+1)$
즉, 이 경우 본 식을 $0$으로 만드는 $\alpha $는 $-\frac{1}{2}$, $-\frac{1}{3}$, $-\frac{1}{4}$로 정수 아닌 유리수가 됩니다. 이렇게 분수꼴로 나타난 이유는 인수분해된 일차식에서 일차항의 계수가 1이 아니라 2, 3, 4가 나왔기 때문이죠. 그리고 양변의 계수 비교에 의해 이 수들을 다음과 같이 모두 곱하면 본 식의 최고차항의 계수와 같아집니다.
$24=2\times 3\times 4$
즉, $\alpha $를 이루는 분모의 값은 최고차항의 계수의 약수중에 하나임을 알 수 있어요.
일반적으로 모든 계수가 정수인 $n$차 다항식 $P(x)=a_0+a_1x+a_2x^2+~\cdots ~+a_nx^n$이 두 정수 $p$, $q$와 $n$개의 정수 $b_0$, $b_1$, $b_2$, $\cdots$ , $b_{n-1}$에 대하여 다음과 같이 인수분해 된다고 가정해 봅시다.
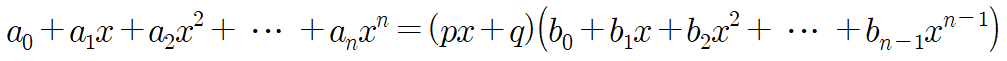
이때, 항등식의 성질에 의해 $P(-\frac{q}{p})=0$이고 계수비교법으로 최고차항끼리 비교하면 $a_n~^n=pb_{n-1}$, 상수항끼리 비교하면 $a_0=qb_0$가 성립합니다. 즉, $p$는 $a_n$의 약수이고, $q$는 $a_0$의 약수임을 알 수 있습니다.
위의 원리에 의해 일반적으로 계수가 정수인 다항식이 일차식 $x-\alpha $와 계수가 정수인 다항식의 곱으로 인수분해된다면 그 $\alpha $는 다음의 범위에서 찾을 수 있습니다.


다항식 $8x ^{3} -12x ^{2} -2x+3$을 계수가 정수인 범위에서 인수분해 하시오.
♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 다항식' 카테고리의 다른 글
| 인수분해를 활용한 복잡한 수의 계산 (고1 수학 다항식) (0) | 2023.07.13 |
|---|---|
| 차순 정리를 이용한 문자가 여러 개인 복잡한 식의 인수분해 (고1수학 다항식) (0) | 2023.07.04 |
| 복이차식 인수분해에 대한 자세한 이해 (고1 수학 다항식) (4) | 2023.06.27 |
| 치환을 이용한 인수분해, 상반다항식의 인수분해 (고1 수학 다항식) (0) | 2023.06.08 |
| 다항식의 인수분해의 개념 및 기초 (고1 수학 다항식) (4) | 2023.05.31 |






댓글 영역