고정 헤더 영역
상세 컨텐츠
본문
인수분해 전략을 활용한 여러 가지 인수분해 공식 유도하기 (고1 수학 다항식)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽게 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
지난 포스팅에서는 인수분해를 다양한 계산 문제에 활용하는 방법을 알아봤는데요. 이 포스팅에서는 지금까지 알아본 인수분해 전략을 이용하여 여러 가지 인수분해 공식을 총 정리해 보도록 하겠습니다. 인수분해 공식은 사실 곱셈공식과 똑같고, 곱셈 공식은 다항식의 곱셈을 공부할 때 인수분해가 되어있는 식을 전개함으로써 결과물을 확인해 봤기 때문에 모든 교과서에서는 인수분해 공식은 별도의 유도과정 없이 제시합니다. 그러나 전개된 식에서 반대방향으로 유도하는 과정을 직접 해보면 그동안 배운 인수분해 전략을 정리할 수 있고 공식을 더 깊이 이해하는데 도움이 될 것입니다.

● 공식 a³-b³=(a-b)(a²+ab+b²) 유도하기 (인수정리 이용)
세제곱 인수분해 중에서 가장 간단하면서도 그 활용도 또한 높은 공식이죠. 우리가 배운 인수분해 전략 중에서도 가장 중요한 게 인수정리이므로 이 방법으로 다음과 같이 간단히 유도할 수 있습니다.
$a=b$를 대입하면 $a^3-b^3=0$이므로 본 식은 $a-b$로 나누어 떨어진다. 따라서 다음 조립제법에 의해
$a^3-b^3=(a-b)(a^2+ab+b^2)$
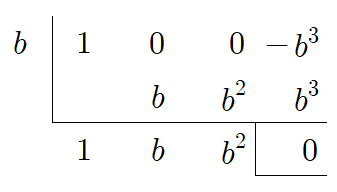
이제 유도한 식에서 $b$ 대신 $-b$를 대입하면 다음의 식도 함께 유도할 수 있습니다.
$a^3+b^3=(a+b)(a^2-ab+b^2)$
● 공식 a³+3a²b+3ab²+b³=(a+b)³ 유도하기 (공식 이용)
세제곱에 대한 첫 번째 인수분해 공식이죠. 이 식은 각 항의 계수가 좌우 대칭을 이루는 상반다항식이므로 $a=-b$를 대입하면 마찬가지로 인수정리를 이용할 수도 있습니다. 그런데 우리가 인수분해 문제를 풀 때 첫 번째로 공부했던 전략이 공식 활용이었죠. 여기서는 위에서 유도한 공식 $a^3+b^3=(a+b)(a^2-ab+b^2)$을 활용하여 이 식을 어렵지 않게 유도할 수 있어요.
이 식은 상반다항식의 특징을 보이므로 계수가 같은 항끼리 묶으면
$a^3+3a^2b+3ab^2+b^3=(a^3+b^3)+(3a^2b+3ab^2)$
$a^3+b^3=(a+b)(a^2-ab+b^2)$로 인수분해하고 정리하면
$(a+b)(a^2-ab+b^2)+(3a^2b+3ab^2)$
$=(a+b)(a^2-ab+b^2)+3ab(a+b)$
$=(a+b) \left\{ (a^2-ab+b^2)+3ab \right\}$
$=(a+b)(a^2+2ab+b^2)=(a+b)(a+b)^2$
$=(a+b)^3$
이제 유도한 식에서 $b$ 대신 $-b$를 대입하면 다음의 식도 함께 유도할 수 있습니다.
$a^3-3a^2b+3ab^2-b^3=(a-b)^3$
● 공식 a²+b²+c²+2ab+2bc+2ca=(a+b+c)² 유도하기 (차순 정리)
위와 같이 문자가 여러 개인 식은 문자 하나를 잡아서 차순으로 정리하면 된다고 배웠죠. 이 식을 $c$에 대하여 내림차순으로 정리하여 인수분해 해보겠습니다. 중간 과정에서 $a+b$를 다른 문자로 치환하면 잘 보이겠지만, 안 해도 이 정도는 할 수 있겠죠?
$a ^{2} +b ^{2} +c ^{2} +2ab+2bc+2ca$
$=c ^{2} +(2a+2b)c+(a ^{2} +2ab+b ^{2})$
$=c ^{2} +2(a+b)c+(a+b)^2$
$=\left\{c+(a+b) \right\}^2$
이제 기본 공식 유도는 다 했습니다. 그런데 사교육계를 들여다보면 인수분해 공식을 이 정도만 알려주고 끝내는 학원은 어디에도 없죠. 이 포스팅을 통해 더 다양한 인수분해 공식도 유도해 보겠습니다.
● 공식 x³+(a+b+c)x²+(ab+bc+ca)x+abc=(x+a)(x+b)(x+c) 유도하기 (차순 정리)
문자가 4개나 되므로 여기서도 필요한 건 차순정리입니다. 위의 식은 $x$에 대하여 차순정리가 되어있는데 그 차수가 높으므로 다른 문자를 잡고 차순정리를 시도하면 돼요. 여기서도 $c$를 기준으로 정리하면 다음과 같이 인수분해 할 수 있습니다.
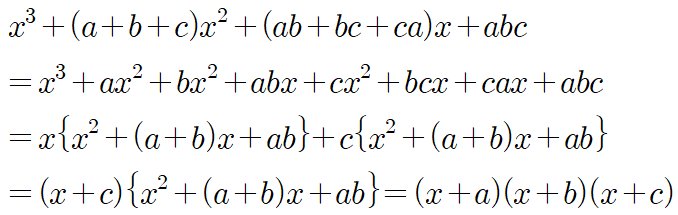
● 공식 a⁴+a²b²+b⁴=(a²-ab+b²)(a²+ab+b²) 유도하기 (A²-B²꼴 치환)
사교육계에서 공식처럼 암기시키는 식인데 하나의 유형으로 생각하시면 됩니다. 공통인수가 보이지 않고 차순정리, 인수정리도 안 통하는 이 식은 $A^2-B^2$ 전략을 이용합니다.
$a ^{4} +a ^{2} b ^{2} +b ^{4}$
$=a ^{4} +$ $2a ^{2} b ^{2}$ $+b ^{4}$ $-a ^{2} b ^{2}$
$=(a^2+b^2)^2-(ab)^2$
$=(a^2-ab+b^2)(a^2+ab+b^2)$
또는 공식 $a^3-b^3=(a-b)(a^2+ab+b^2)$을 응용하여 다음과 같이 유도할 수도 있어요.
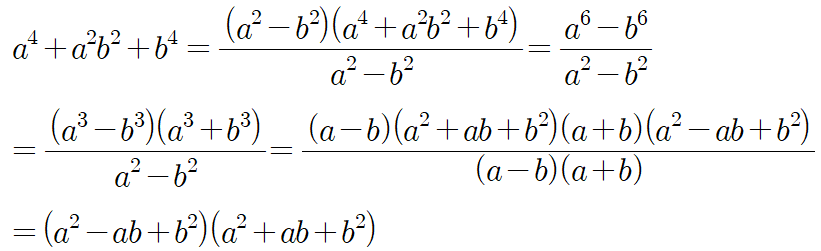
● 공식 (a+b+c)(ab+bc+ca)-abc=(a+b)(b+c)(c+a) 유도하기 (차순 정리)
다음은 네이버 지식백과에서 제시하는 인수분해 공식들입니다.

가운데에 유도할 식이 제시된 게 보이죠. 이 식도 공식이라기보다는 하나의 유형으로 보시면 됩니다. 문자가 여러 개이므로 다음과 같이 $a$를 기준으로 정리하여 인수분해 할 수 있습니다.
$(a+b+c)(ab+bc+ca)-abc$
$= \left\{a+(b+c) \right\} \left\{a(b+c)+bc \right\}-abc$
$= (b+c)a^2+(b+c)^2a+abc+bc(b+c)-abc$
$= (b+c)a^2+(b+c)^2a+bc(b+c)$
$= (b+c)\left\{a^2+(b+c)a+bc \right\}$
$= (b+c)(a+b)(a+c)=(a+b)(b+c)(c+a)$
● 공식 a³+b³+c³-3abc=(a+b+c)(a²+b²+c²-ab-bc-ca) 유도하기 (종합)
이제 끝판왕 공식이 남았습니다. 결과 차제가 길어서 반대로 전개하는 게 오히려 더 복잡한 공식이에요. 이걸 어떻게 인수분해할까 싶지만 곱셈 변형식 $a^3+b^3=(a+b)^3-3ab(a+b)$와 $a^3+b^3=(a+b)(a^2-ab+b^2)$을 차례대로 이용하면 다음과 같이 몇 줄 안 쓰고 유도할 수 있습니다.
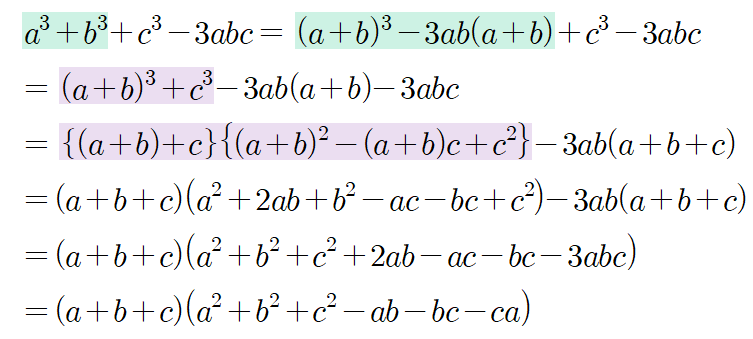

위의 인수분해 결과에서 식 $a ^{2} +b ^{2} +c ^{2} -ab-bc-ca$는 곱셈 공식의 변형 파트를 공부할 때 다음과 같이 변형할 수 있음을 알아봤습니다. (관련 글: https://holymath.tistory.com/entry/다항식-곱셈공식의-다양한-활용문제)
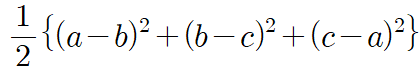
이 식은 $a=b=c$일 경우 0이 되는 특징을 가지고 있죠. 즉, 주어진 인수분해 공식은 $a+b+c=0$이거나 $a=b=c$이면 0이 되므로 다음과 같이 정리할 수도 있습니다.
$a+b+c=0$ 또는 $a=b=c$이면 $a^3+b^3+c^3=3abc$ |

다음 식을 인수분해 하시오.
$(x-y)^3+(y-z)^3+(z-x)^3$
세제곱식 안에 들어있는 $x-y$, $y-z$, $z-x$를 각각 $A$, $B$, $C$로 치환하면 다음이 성립합니다.
$A+B+C=(x-y)+(y-z)+(z-x) =0$
따라서 위에서 정리한 식 $a^3+b^3+c^3=3abc$에다 문제의 식을 대입하면 다음과 같이 인수분해됩니다.
$(x-y)^3+(y-z)^3+(z-x)^3=3(x-y)(y-z)(z-x)$
♥ 이해가 잘 되셨다면 좋아요와 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 다항식' 카테고리의 다른 글
| 인수분해를 활용한 복잡한 수의 계산 (고1 수학 다항식) (0) | 2023.07.13 |
|---|---|
| 차순 정리를 이용한 문자가 여러 개인 복잡한 식의 인수분해 (고1수학 다항식) (0) | 2023.07.04 |
| 인수정리를 이용한 인수분해에 대한 자세한 이해 (고1수학 다항식) (0) | 2023.06.30 |
| 복이차식 인수분해에 대한 자세한 이해 (고1 수학 다항식) (4) | 2023.06.27 |
| 치환을 이용한 인수분해, 상반다항식의 인수분해 (고1 수학 다항식) (0) | 2023.06.08 |





댓글 영역