유리함수 y=k/x의 그래프에 대한 자세한 이해 (고1수학 함수)

 

 

유리함수 y=k/x의 그래프에 대한 자세한 이해 (고1수학 함수)

우리는 중학교 1학년 때 반비례 함수의 그래프를 배운 적이 있습니다. (자료 출처: 미래엔 중학 수학1)

 

 안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.

 지난 포스팅에서 유리함수의 개념에 대해 배웠습니다. 이번 포스팅에서는 고등학교에서 다루는 기본적인 유리함수의 그래프에 대해 알아보도록 하겠습니다.

 

● y=k/x의 그래프의 특징

유리함수는 다항식과 다항식의 비로 이루어진 유리식으로 된 함수이므로 이러한 유리함수의 종류는 무수히 많으며, 그 종류에 따라 그래프도 다양하게 나타납니다. 따라서 이런 형태의 함수를 다 배울 수는 없고 고등학교 1학년 수준에서는 다항함수가 아닌 유리함수 중에서 가장 간단한 형태의 유리함수만 공부합니다. 그리고 지난 포스팅에서도 언급했듯이 그 간단한 형태의 유리함수는 중학교 1학년 때 배웠고, 위의 대표 이미지로 소개한 반비례 함수부터 시작합니다.

그림 출처: 좋은책 신사고

반비례 함수는 $y=\frac{k}{x}(k\ne 0)$꼴의 함수로 $x$가 2배, 3배, 4배, $\cdots$로 변하면 $y$는 $\frac{1}{2}$배, $\frac{1}{3}$배, $\frac{1}{4}$배로 변하는 함수를 말합니다.

분모를 다른 쪽 변으로 보내면 $xy=k$의 꼴이 되고 $k$는 $0$이 아니므로 $x$와 $y$ 둘 다 $0$이 될 수 없어요. 따라서 반비례 함수의 정의역과 치역은 모두 $0$을 제외한 실수 전체의 집합이 됩니다.

$k$가 양수이면 $xy>0$이므로 $x$와 $y$는 둘 다 양수이거나 둘 다 음수입니다. 따라서 그래프는 제1사분면과 제3사분면을 지나게 됩니다. 반대로 $k$가 음수이면 $xy<0$이므로 $x$와 $y$는 부호가 다르죠. 따라서 그래프는 제2사분면과 제4사분면을 지나게 됩니다.

그리고 방정식 $xy=k$는 $x$, $y$에 각각 $-x$, $-y$를 대입해도 결과는 같고 $x$, $y$를 서로 바꾸어도 그 결과는 같죠. 이 두 작업을 동시에 해도 마찬가지예요. 즉, 반비례 함수의 그래프는 원점에 대하여 대칭이고 직선 $y=x$에 대해서도 대칭입니다. 즉, 이 함수의 역함수는 자기 자신이란 뜻이죠. 추가적으로 직선 $y=-x$에 대해서도 대칭을 이룹니다.

함수 식 $y=\frac{k}{x}(k\ne 0)$에서 $x$의 절댓값이 커지면 커질수록 $y$의 값은 점점 $0$에 가까워집니다. 그리고 식을 $x=\frac{k}{y}(k\ne 0)$로 고쳐서 보면 $y$의 절댓값이 커질 때도 역시 $x$의 값이 점점 $0$에 가까워짐을 알 수 있습니다. 따라서 이 함수의 그래프는 두 직선 $x=0$와 $y=0$ 즉, $x$축, $y$축에 한없이 가까워지는 모습을 띱니다. 한없이 가까워지지만, $x$나 $y$가 $0$이 되지는 않으므로 결코 $x$축이나 $y$축에 그래프가 닿는 일은 생기지 않죠. 

이렇게 곡선 위의 점이 어떤 직선에 한없이 가까워질 때, 이 직선을 그 곡선의 점근선이라고 합니다. 반비례 함수에서는 다음과 같이 $x$축과 $y$축이 점근선이 되죠. 이렇게 점근선은 대체로 아무리 가까이 가도 결코 만날 수 없는 슬픈 관계를 보입니다.

이때 $y=\frac{k}{x}(k\ne 0)$에서 $k$의 절댓값이 작으면 $x$의 절댓값이 커질 때 $y$는 좀 더 빨리 $0$에 가까워지고, $k$의 절댓값이 크면 $y$는 좀 더 천천히 $0$에 가까워지겠죠. 따라서 처음에 제시한 그래프를 다시 보면 반비례 함수의 그래프는 $k$의 절댓값이 작을수록 그 그래프는 $x$축, $y$축 그리고 원점에 더욱 가까워진다는 것도 알 수 있어요.

그림 출처: 좋은책 신사고

간단한 식으로 만든 그래프이지만 다양한 특징들을 꽤나 많이 발견할 수 있죠. 지금까지 얘기한 내용을 다음과 같이 정리할 수 있습니다.

■ 유리함수 $y=\frac{k}{x}(k\ne 0)$의 그래프

① 정의역과 치역은 모두 0이 아닌 실수 전체의 집합이다. ② $k>0$이면 그래프는 제1사분면, 제2사분면에 있고, $k<0$이면 그래프는 제2사분면, 제4사분면에 있다. ③ 원점, 직선 $y=x$, 직선 $y=-x$에 대하여 대칭이다. ④ 점근선은 $x$축, $y$축이다. ⑤ $k$의 절댓값이 작을 수록 그래프는 $x$축, $y$축, 원점에 가까워진다.

 

유리함수의 그래프는 직선이 아닌 곡선이므로 그 그래프를 보다 정확하게 그리기 위해서는 점을 많이 찍어줄 필요가 있고, 그 점을 연결하는 연습을 반복적으로 해보면서 스스로 감을 잡아야 합니다. 다음은 지오지브라를 이용하여 유리함수의 그래프를 나타낸 것입니다. 출처에 안내된 링크로 들어가면 왼쪽 목록에서 a값을 표시한 첫 번째 동그라미와 함수 식이 있는 네 번째 동그라미를 눌러서 활성화 한 다음 슬라이더를 움직이면서 유리함수의 그래프를 관찰할 수 있습니다.

자료 출처: https://www.geogebra.org/m/mq2jpxtq

 

● y=k/x의 그래프 관련 연습 문제 풀이

 

그림과 같이 원점을 지나는 직선 $l$과 함수 $y=\frac{2}{x}$의 그래프가 두 점 P, Q에서 만난다. 점 P를 지나고 $x$축에 수직인 직선과 점 Q를 지나고 $y$축에 수직인 직선이 만나는 점을 R라 할 때, 삼각형 PQR의 넓이는?  [2017.11/3점]

① $4$     ② $\frac{9}{2}$     ③ $5$     ④ $\frac{11}{2}$     ⑤ $6$

문제를 가만히 읽어보면 직선 $l$은 원점을 지난다는 조건만 주어져 있고 기울기는 나와있지 않습니다. 그런데 삼각형 PQR의 넓이를 구하라는 것은 결국 기울기가 얼마이든 상관없이 구하는 넓이가 일정하다는 것이죠. 따라서 직선의 기울기를 1로 놓고 그림과 같이 교점을 이으면 삼각형 PQR은 한 변의 길이가 $2\sqrt{2}$인 직각이등변삼각형이 됨을 알 수 있어요. 그럼 넓이는 $\frac{1}{2}\times (2\sqrt{2}{)}^2=4$임을 바로 알 수 있습니다.

이러한 전략을 '특수화'라고 부릅니다. 실전에서는 이렇게 풀 수 있고 개념 공부를 위해 다음과 같이 접근할 수 있습니다.

이상으로부터 답은 ①번입니다.

---

 

그림과 같이 함수 $y=\frac{4}{x}$의 그래프 위의 점 중 제1사분면에 있는 한 점을 $\text{A}(a,\frac{4}{a})$라 하고, 점 $\text{A}$를 $x$축, $y$축, 원점에 대하여 대칭이동한 점을 각각 $\text{B}$, $\text{C}$, $\text{D}$라 하자. 직사각형 $\text{ACDB}$의 둘레의 길이의 최솟값은?  [2016.06/3점]

① $10$     ② $12$     ③ $14$     ④ $16$     ⑤ $18$

 유리함수는 다른 개념을 끌어다가 섞어서 출제하는 경우가 많습니다. 여기서는 그림과 같이 길이를 표시하고 둘레의 식을 구하면 다음과 같습니다.

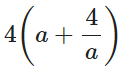
즉, 우리에게 필요한 건 $a$가 양수일 때 위의 식의 최솟값을 구하는 겁니다. 그럼 뭘 써먹어야 하는지 떠오르시나요? 바로 절대부등식에서 공부했던 산술·기하 부등식이죠.

 여기서 등호는 $a=2$일 때 성립합니다. 그리고 구하는 최솟값은 이 식의 4배이므로 $16$이 되죠. 결국, 이 경우에도 최소가 될 조건은 주어진 사각형이 직선 $y=x$의 일부를 대각선으로 갖는 정사각형인 경우라는 걸 알 수 있어요.

이상으로부터 답은 ④번입니다.

---

 

그림과 같이 유리함수 $y=\frac{k}{x}(k>0)$의 그래프가 직선 $y=-x+6$과 두 점 P, Q에서 만난다. 삼각형 OPQ의 넓이가 $14$일 때, 상수 $k$의 값은? (단, O는 원점이다.)  [2016.03/4점]

① $\frac{32}{9}$     ② $\frac{34}{9}$     ③ $4$     ④ $\frac{38}{9}$     ⑤ $\frac{40}{9}$

 

접근하는 방법은 다양하게 있는데 저는 이 함수의 그래프가 직선 $y=x$에 대하여 대칭임을 이용하여 다음과 같이 접근해 보겠습니다.

그림처럼 직선 위의 점 $(3,3)$을 잡으면 이 점과 원점을 연결한 파란색 선분의 길이는 $3\sqrt{2}$가 되고 직선 PQ와 수직입니다. 따라서 이 선분이 삼각형 OPQ의 높이가 되고 이 삼각형의 넓이가 $14$이므로

$\frac{1}{2}\times \overline{\text{PQ}}\times 3\sqrt{2}=14$

로부터 $\overline{\text{PQ}}=\frac{14}{3}\sqrt{2}$입니다.

이 길이의 절반이 $\frac{7}{3}\sqrt{2}$이므로 다음과 같이 $x$축에 수선의 발을 내려서 각 길이를 구하면 점 P의 좌표를 구할 수 있겠죠. 도형이 직선 $y=x$에 대하여 대칭이니까 점 Q의 좌표를 대신 구할 수도 있습니다.

따라서 점 P의 $x$좌표는 $3+\frac{7}{3}=\frac{16}{3}$이고 점 P는 직선 $y=-x+6$ 위의 점이므로 $y$좌표는 $y=-\frac{16}{3}+6=\frac{2}{3}$입니다.

이제 마지막입니다. 점 P는 곡선 $y=\frac{k}{x}$ 위의 점이므로 $xy=k$로부터

$k=\frac{16}{3}\times \frac{2}{3}=\frac{32}{9}$

따라서 답은 ①번입니다.

---

 

♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.