유리함수 y=(ax+b)/(cx+d)에 대한 자세한 이해 (고1 수학 함수 개념)

유리함수 y=(ax+b)/(cx+d)에 대한 자세한 이해 (고1 수학 함수 개념)

행성의 회합주기는 태양을 중심으로 행성이 지구와 일직선을 이루는 주기를 말합니다. 태양으로부터 지구보다 멀리 떨어진 외행성의 공전주기를 x라 하면 이 행성과 지구가 태양과 일직선을 이루는 주기는 유리함수 365x/(x-365) (일)로 표현할 수 있습니다.

 

 안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.

 지난 포스팅에서 y=k/(x-p)+q 형태의 유리함수의 그래프를 탐구하였습니다. 이제 고등학교 유리함수 유형의 마지막 단계로 일차식과 일차식의 비로 이루어진 y=(ax+b)/(cx+d) 형태의 유리함수에 대해 알아보도록 하겠습니다.

● y=(ax+b)/(cx+d)와 y=k/(x-p)+q의 관계

이전부터 조금씩 언급했는데 $y=\frac{ax+b}{cx+d}$형태의 유리함수는 $y=\frac{k}{x-p}+q$형태의 유리함수 식을 통분하여 하나의 분수로 나타낸 함수입니다. 따라서 이런 함수의 성질을 분석하려면 다음과 같이 $y=\frac{k}{x-p}+q$의 형태로 되돌려주면 됩니다.

출처: EBS 수학의 왕도 수학 하

 위의 예시처럼 함수 $y=\frac{2x+5}{x+1}$는 수식을 $y=\frac{3}{x+1}+2$로 바꿀 수 있어요. 그리고 이 함수는 $y=\frac{3}{x}$의 그래프를 $x$축의 방향으로 $-1$만큼, $y$축의 방향으로 $2$만큼 평행이동한 것이므로 결국 함수 $y=\frac{2x+5}{x+1}$의 그래프는 함수 $y=\frac{3}{x}$의 그래프와 합동이 됩니다.

 그리고 이러한 과정에는 다음과 같이 앞에서 배운 다항식의 나눗셈 개념이 이용됩니다. 즉, 몫이 붙어있는 식은 나누어 떨어지므로 말 그대로 분수 밖으로 떨어져 나가고, 나머지는 말 그대로 분자에 그대로 남게 됩니다.

 이런 식으로 풀어내면 결국 $y=\frac{ax+b}{cx+d}$형태의 유리함수 또한 $y=\frac{k}{x}$형태의 반비례 함수의 그래프를 평행이동시켜서 만들 수 있는 함수가 됩니다.

출처: EBS 수학의 왕도 수학 하

 

● y=(ax+b)/(cx+d)가 어떤 y=k/x의 그래프와 합동이 되기 위한 조건

단, 함수 $y=\frac{ax+b}{cx+d}$에서 상수 $a$, $b$, $c$, $d$가 어떠한 값이든 그래프가 반비례 함수와 합동이 되도록 그려지는 것은 아니에요. 학생 여러분이 공부하는 교과서를 보시면 해당 내용에는 $ad-bc\ne 0$와 $c\ne 0$라는 조건이 따라붙습니다. 그럼 이 조건이 왜 필요한지 알아보겠습니다.

우선 $c\ne 0$라는 조건은 간단히 확인할 수 있어요. 만약 $c=0$이 되면 함수 $y=\frac{ax+b}{cx+d}$는 $y=\frac{ax+b}{d}$가 됩니다. 즉, 분모가 상수가 되죠. 그럼 이 함수는 일차함수가 되므로 그래프는 곡선이 아니라 직선으로 그려지게 됩니다.

이제 $c\ne 0$임을 전제로 하고 식 $\frac{ax+b}{cx+d}$를 직접 나눗셈을 하여 $\frac{k}{x-p}+q$의 꼴로 바꿔보면

여기서 $ad-bc=0$일 경우 양변을 $-c$로 나누면

이것은 다음과 같이 주어진 함수를 상수함수로 만들게 됩니다.

즉, $ax+b$, $cx+d$의 비가 이들의 최고차항의 계수 $a$, $c$의 비로 일정한 값을 갖게 되는 거죠. 예를 들면 $\frac{4x+2}{2x+1}=2$가 되는 두 식 $4x+2$, $2x+1$에서 $ad-bc$를 계산하면 $4\times 1+2\times 2=0$이 됩니다.

따라서 이런 경우는 함수 $y=\frac{ax+b}{cx+d}$가 상수함수가 되어 그래프가 역시 직선을 그립니다. 완전한 직선은 아니고 분모가 $0$이 되는 점 $(-\frac{d}{c},\frac{a}{c})$는 뚫려있는 직선이 되죠.

물론 $c=0$로 인한 일차함수나 $ad-bc=0$로 인한 상수함수 모두 유리함수임에는 변화가 없어요. 단, 유리함수 $y=\frac{ax+b}{cx+d}$의 그래프가 우리가 배운 반비례 함수의 그래프처럼 십자가 모양의 점근선을 따라 곡선이 그려지도록 하려면 $ad-bc\ne 0$와 $c\ne 0$이라는 조건이 따라야만 합니다.

 

유리함수 $y=\frac{2x-3}{x-4}$의 그래프에서 점근선의 방정식이 $x=p$, $y=q$일 때, $p+q$의 값은?  [2015(고2).03/3점]

① $6$     ② $7$     ③ $8$     ④ $9$     ⑤ $10$

다음과 같이 분자를 분모로 나누어서 나타냅니다.

따라서 점근선은 $x=4$와 $y=2$이므로 $p+q=4+2=6$입니다.

따라서 답은 ①번입니다.

---

 

함수 $y=\frac{ax+b}{x+c}$의 그래프가 다음과 같을 때 상수 $a$, $b$, $c$대하여 $abc$의 값을 구하시오.  [좋은책 신사고 수학 변형]

주어진 식을 해석하여 그래프를 그릴 줄 아는 것도 중요하지만, 수학에서는 항상 거꾸로 생각하는 능력도 중요하게 다루어집니다. 이 문제처럼 그래프를 먼저 갖다 놓고 이걸 그려내는 수식을 추론하는 방식도 역발상에 해당되죠.

이런 문제에서도 핵심은 역시 점근선입니다. 구하려는 함수의 식에는 미지수가 3개나 되지만 점근선이 $x=2$, $y=1$임을 이용하여 주어진 함수의 식을 다음과 같이 바꾸면 미지수는 1개로 줄어듭니다.

이제 $k$의 값을 구하기 위해 그래프를 통해 이 함수의 특징을 하나만 더 찾으면 되겠죠. $y$절편이 $2$이므로 점 $(0,2)$를 지난다는 것을 이용하면

   $2=\frac{k}{-2}+1$
   $\frac{k}{-2}=1$
   $k=-2$

이렇게 해서 함수의 식을 완성할 수 있습니다. 이제 이 식을 다시 통분하면

따라서 $a=1$, $b=-4$, $c=-2$이므로 $abc=8$입니다.

---

 

그림과 같이 $\overline{\mathrm{AB}}=\overline{\mathrm{BC}}=\overline{\mathrm{CD}}=2$, $\overline{\mathrm{AD}}=3$인 등변사다리꼴 $\mathrm{ABCD}$에서 선분 $\mathrm{BC}$ 위를 움직이는 점을 $\mathrm{E}$, 직선 $\mathrm{AE}$와 직선 $\mathrm{CD}$의 교점을 $\mathrm{F}$라 하자. 점 $\mathrm{C}$와 점 $\mathrm{E}$ 사이의 거리를 $x(0\le x\le 2)$, 점 $\mathrm{C}$와 점 $\mathrm{F}$ 사이의 거리를 $f(x)$라 할 때, 함수 $y=f(x)$의 그래프의 모양으로 알맞은 것은?  [2015(고2).09/4점]

 

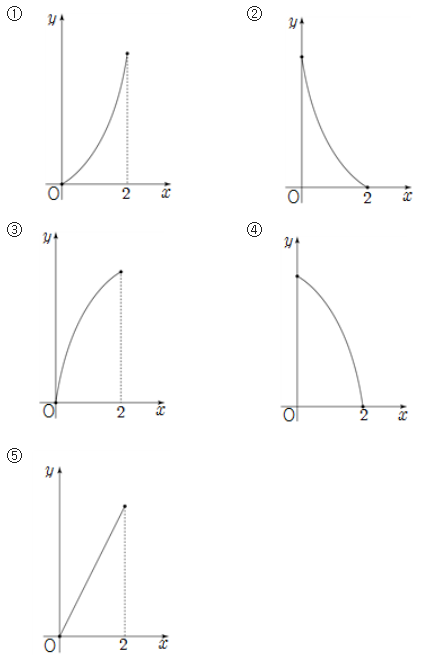
이 문제에서 핵심 아이디어는 $f(x)$와 $x$의 관계를 파악하는 겁니다. 그래서 이 관계를 구하기 위해 필요한 원리는 두 삼각형 $\mathrm{AFD}$와 $\mathrm{EFC}$가 닮음이라는 점입니다. 따라서 다음의 비례식이 성립합니다.

    $\overline{\mathrm{AD}}:\overline{\mathrm{EC}}=\overline{\mathrm{DF}}:\overline{\mathrm{CF}}$

    $3:x=f(x)+2:f(x)$

    $xf(x)+2x=3f(x)$
    $(x-3)f(x)=-2x$
    $f(x)=\frac{-2x}{x-3}$
    $=\frac{-2(x-3)-6}{x-3}$
    $=\frac{-6}{x-3}-2$

따라서 $y=f(x)$의 그래프는 두 직선 $x=3$, $y=-2$을 점근선으로 하며 점근선으로 나누어진 네 영역 중 왼쪽 윗부분과 오른쪽 아랫부분에 곡선이 그려지는 형태입니다. 단, $0\le x\le 2$의 범위에서만 그려지죠.

또한, $f(x)=\frac{-2x}{x-3}$이므로 그래프는 원점을 지납니다.

따라서 이를 만족하는 그래프는 ①번입니다.

---

 

♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.