고정 헤더 영역
상세 컨텐츠
본문

수학으로 사랑 고백하는 법 (고1 수학 원의 방정식, 무리함수로 완벽한 하트 모양의 그래프 그리기)


안녕하세요? holymath입니다. 최근 무리함수를 주제로 포스팅을 몇 개 올렸는데요. 오늘의 포스팅에서는 무리함수의 그래프와 이전에 배웠던 원의 방정식으로 구현할 수 있는 하트 모양의 그래프를 알아보도록 하겠습니다.

● 들어가기
좋아하는 이성한테서 메신저 톡으로 하트 이모티콘을 받는 것만큼 설레는 일은 없겠죠? 서두에 첨부한 그림처럼 일상에서도 하트 모양은 어렵지 않게 만날 수 있습니다.

이러한 모양은 수학을 통해서도 그릴 수 있는데요. 인터넷에 검색해 보면 가장 많이 등장하는 식이

여기에다

그다음으로 자주 볼 수 있는 방정식은 극좌표를 이용한 방정식
그림과 같은 점

이러한 원리를 바탕으로 방정식

여기까지가 대중적으로 알려진 하트 방정식인데 고등학생이 이해하기엔 좀 어렵죠. 그리고 하트 모양도 뭔가 좀 아쉽습니다. 지금부터는 고등학교 1학년에서 배운 개념만 가지고 보다 예쁜 하트 모양의 그래프를 그려보도록 하겠습니다.
● 원의 방정식으로 하트의 윗부분 만들기
하트의 모양은 윗부분의 움푹 파인 부분이 포인트죠. 이 부분을 다음과 같은 함수를 통해 구현할 수 있습니다.
다소 복잡해 보이지만 루트를 풀어서 일반형으로 나타내면 다음과 같이 우리가 아는 방정식이 등장합니다.
단, 처음에 무리함수로 주어졌으므로 루트 안의 식이 음수가 되면 안 되죠. 따라서 정의역에 다음과 같이 제한이 걸립니다.
또한,
따라서
이상으로부터 함수

● 무리함수로 하트의 아랫부분 만들기
이제 다음과 같은 무리함수를 생각해 봅시다.
정의역과 치역을 살펴보면
따라서
이므로
특히,

따라서 절댓값 기호를 붙인

● 완성된 하트 그래프
이제 거의 다 왔죠? 최종적인 하트 그래프를 완성하기 위해서는 다음 두 함수의 그래프를 동시에 그리면 됩니다.
만약 방정식으로 나타내고 싶으면 위와 같이 표현할 경우 연립방정식이 되면서 두 식을 동시에 만족하는 점 두 개만 찍게 되어버리죠. 조금 복잡해 보이지만 다음과 같이 써주면 하나의 방정식으로 표현이 가능합니다.
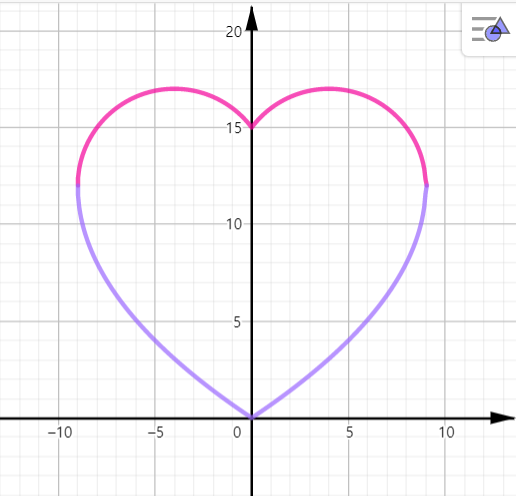
완성된 그래프는 다음과 같습니다. 마음에 드시나요? 어렵고 딱딱해 보이는 수학도 이렇게 감성 어린 표현이 가능하답니다.
♥ 이해가 잘 되셨다면 좋아요와 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 함수' 카테고리의 다른 글
| 무리함수 y=±√(ax+b)+c의 그래프에 대한 자세한 이해 (고1 수학 함수) (5) | 2023.09.16 |
|---|---|
| 무리함수 y=±√ax의 그래프에 대한 자세한 이해 (고1 수학 함수) (0) | 2023.09.08 |
| 무리식, 무리함수에 대한 자세한 이해 (고1 수학 함수) (0) | 2023.08.29 |
| 유리함수의 역함수 구하는 법, 역함수의 특징 (고1 수학 함수 개념) (0) | 2023.02.20 |
| 유리함수 y=(ax+b)/(cx+d)에 대한 자세한 이해 (고1 수학 함수 개념) (7) | 2022.12.15 |





댓글 영역