고정 헤더 영역
상세 컨텐츠
본문
무리함수 y=±√(ax+b)+c의 그래프에 대한 자세한 이해 (고1 수학 함수)

안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽게 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
지난 포스팅에서 $y=\sqrt{ax}$ 꼴의 무리함수의 그래프의 특징을 알아보았습니다. 여기서는 무리함수 식의 형태를 확장하여 $y=\sqrt{ax+b}+c$ 꼴의 무리함수의 그래프에 대해 알아보겠습니다.

● 무리함수 그래프의 평행이동
지난 포스팅에서 알아본 무리함수의 그래프의 특징은 다음과 같이 4가지로 분류됩니다.
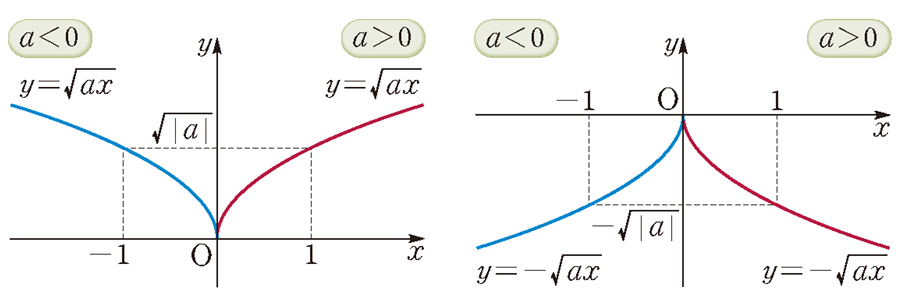
여기서 무리함수를 $x$축의 방향으로 $p$만큼, $y$축의 방향으로 $q$만큼 평행이동시키면 함수의 수식은 다음과 같이 변하겠죠.
$y=\sqrt{ax}$ ─▶ $y-q=\sqrt{a(x-p)}$
$y=\sqrt{ax}$ ─▶ $y=\sqrt{a(x-p)}+q$
그리고 그래프는 다음과 같이 변합니다. 그래프 예시는 $p$, $q$가 둘 다 양수인 경우입니다.
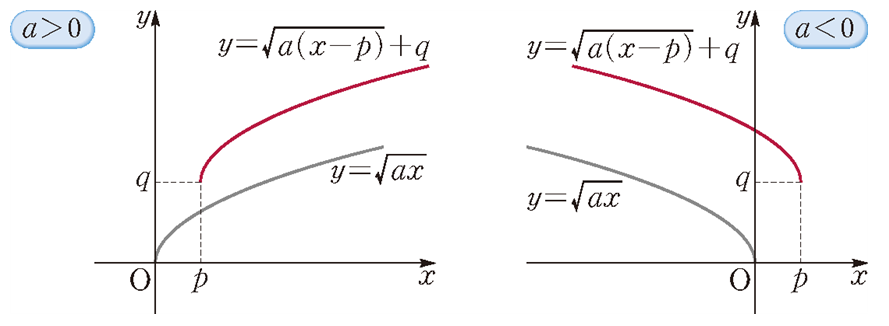
이렇게 함수의 그래프가 전체적으로 바뀌면 그에 따라서 정의역과 치역도 모두 바뀌게 됩니다.
| 구분 | $a>0$ | $a<0$ |
| $y=\sqrt{ax}$의 정의역 | $\left\{x~|~x\geq 0 \right\}$ | $\left\{x~|~x\leq 0 \right\}$ |
| $y=\sqrt{ax}$의 치역 | $\left\{y~|~y\geq 0 \right\}$ | $\left\{y~|~y\geq 0 \right\}$ |
| $y=\sqrt{a(x-p)}+q$의 정의역 | $\left\{x~|~x\geq p \right\}$ | $\left\{x~|~x\leq p \right\}$ |
| $y=\sqrt{a(x-p)}+q$의 치역 | $\left\{y~|~y\geq q \right\}$ | $\left\{y~|~y\geq q \right\}$ |
식 앞에 마이너스를 붙임 함수 $y=-\sqrt{ax}$의 경우도 $x$축의 방향으로 $p$만큼, $y$축의 방향으로 $q$만큼 평행이동시키면 수식은 다음과 같이 변합니다.
$y=-\sqrt{ax}$ ─▶ $y-q=-\sqrt{a(x-p)}$
$y=\sqrt{ax}$ ─▶ $y=-\sqrt{a(x-p)}+q$
그리고 그래프와 정의역 및 치역은 다음과 같이 바뀝니다. 아래의 그래프는 $p$는 양수, $q$는 음수인 경우입니다.
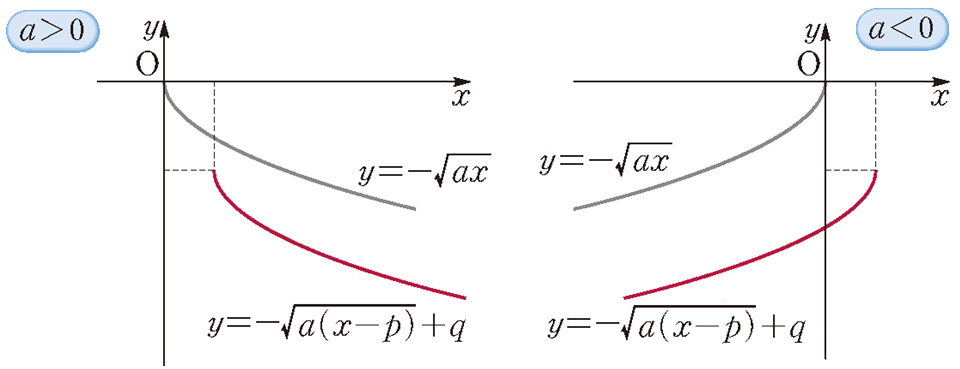
| 구분 | $a>0$ | $a<0$ |
| $y=-\sqrt{ax}$의 정의역 | $\left\{x~|~x\geq 0 \right\}$ | $\left\{x~|~x\leq 0 \right\}$ |
| $y=-\sqrt{ax}$의 치역 | $\left\{y~|~y\leq 0 \right\}$ | $\left\{y~|~y\leq 0 \right\}$ |
| $y=-\sqrt{a(x-p)}+q$의 정의역 | $\left\{x~|~x\geq p \right\}$ | $\left\{x~|~x\leq p \right\}$ |
| $y=-\sqrt{a(x-p)}+q$의 치역 | $\left\{y~|~y\leq q \right\}$ | $\left\{y~|~y\leq q \right\}$ |
예를 들어, 함수 $y=\sqrt{3(x-2)}+1$의 그래프는 함수 $y=\sqrt{3x}$의 그래프를 $x$축의 방향으로 $2$만큼, $y$축의 방향으로 $1$만큼 평행이동한 것으로 그 그래프는 다음과 같습니다.
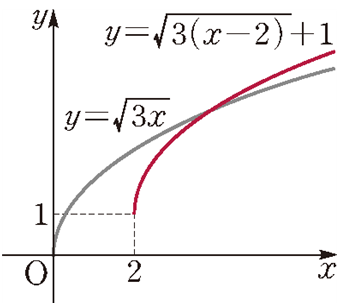
따라서 이 함수의 정의역은 $\left\{x~|~x\geq 2 \right\}$, 치역은 $\left\{y~|~y\geq 1 \right\}$입니다. 또한, 그래프가 시작되는 점이 원점에서 $(2,~1)$로 옮겨졌다는 사실도 알 수 있습니다.

$1 \leq x \leq3$에서 무리함수 $f(x)=\sqrt{x}+a$의 최솟값이 $6$일 때, 상수 $a$의 값은? [2015/11월학평/3점]
① $1$ ② $2$ ③ $3$ ④ $4$ ⑤ $5$
주어진 함수의 그래프는 $f(x)=\sqrt{x}$의 그래프를 $y$축의 방향으로 $a$만큼 평행이동한 것과 같습니다. 따라서 다음과 같이 증가하는 형태로 나타납니다.
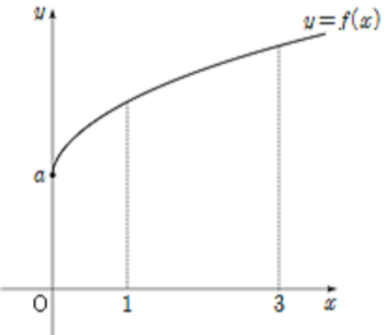
따라서 $1 \leq x \leq3$에서 이 함수는 $x=1$일 때 최솟값 $6$을 가지므로
$f(1)=1+a=6$
따라서 $a=5$이므로 답은 ⑤번입니다.
● 무리함수 y=±√(ax+b)+c의 그래프
고등학교 수준에서 다루는 무리함수는 제목과 같이 근호 안에 일반적인 일차식이 들어가는 수준까지만 다룹니다. 그리고 이런 함수는 $y=\pm \sqrt{ax}$의 그래프를 평행이동하면서 만들 수 있습니다.
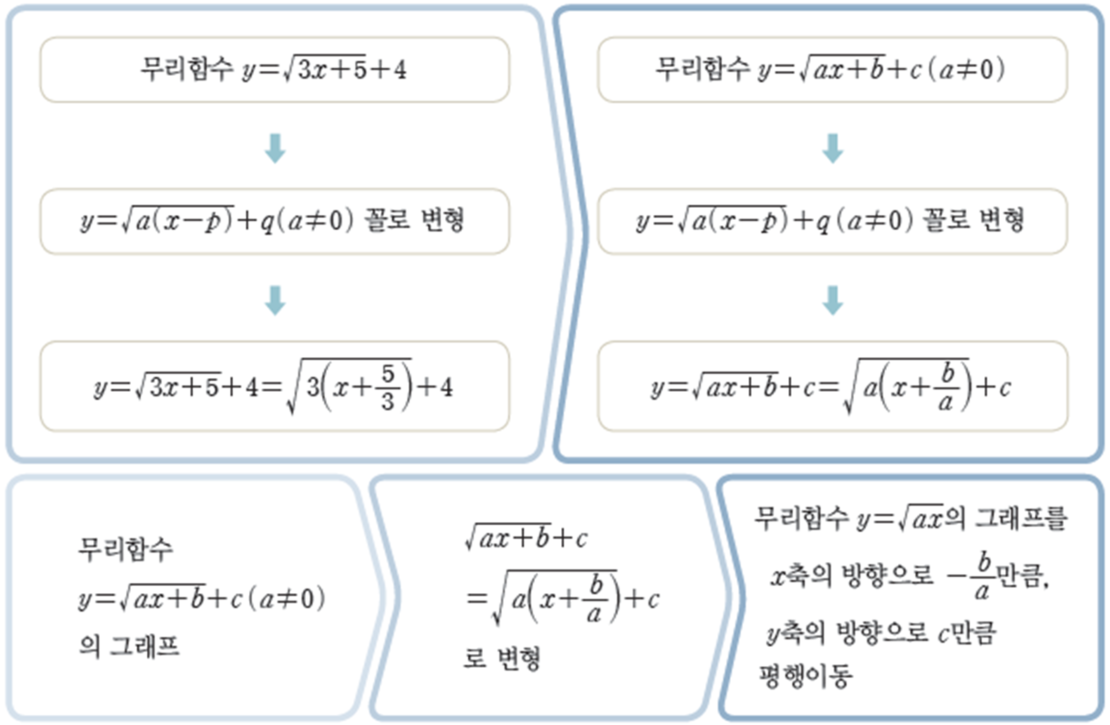
즉 위의 내용에 의해 무리함수 $y= \sqrt{3x+5}+4$의 그래프는 무리함수 $y= \sqrt{3x}$의 그래프를 $x$축의 방향으로 $-\frac{5}{3}$만큼, $y$축의 방향으로 $4$만큼 평행이동한 것과 같습니다.


그림과 같이 무리함수 $y= \sqrt{-2x+4}+a$의 그래프가 두 점 $(b,~1)$, $(0,~3)$을 지날 때, 두 상수 $a$, $b$의 합 $a+b$의 값은? [2014/고1/11월학평/3점]
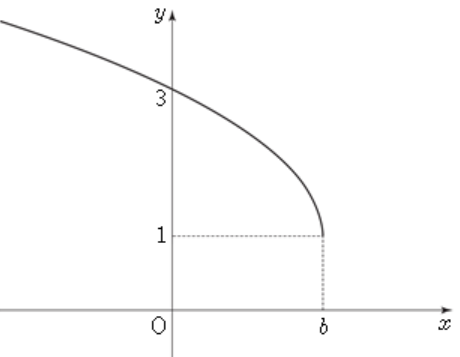
① $3$ ② $4$ ③ $5$ ④ $6$ ⑤ $7$
$y= \sqrt{-2x+4}+a= \sqrt{-2(x-2)}+a$
이므로 그래프의 시작점인 $(b,~1)$은 $(2,~a)$와 같습니다.
그럼 $a=1$, $b=2$임을 바로 구할 수 있으므로 $a+b=3$이죠. 따라서 답은 ①입니다.

다음 중 함수 $y=-\sqrt{3x-6}+3$에 대한 설명으로 옳지 않은 것은? [2015 좋은책 신사고 수학]
① 정의역은 $\left\{x~|~x\geq 2 \right\}$이다.
② 치역은 $\left\{y~|~y\leq 3 \right\}$이다.
③ 그래프는 함수 $y=-\sqrt{3x}$의 그래프를 $x$축의 방향으로 $-2$만큼, $y$축의 방향으로 $3$만큼 평행이동한 것이다.
④ 그래프는 제2사분면, 제3사분면을 지나지 않는다.
⑤ 역함수는 $y=\frac{1}{3} x^2-2x+5~(x\leq 3)$이다.
주어진 함수의 수식을 $y=-\sqrt{a(x-p)}+q$의 꼴로 정리하면
$y=-\sqrt{3x-6}+3=-\sqrt{3(x-2)}+3$
따라서 그래프가 시작되는 점은 $(2,~3)$입니다. 여기를 원점으로 생각하고 함수 $y=-\sqrt{3x}$의 그래프를 그린다면 다음과 같이 오른쪽 아래 방향으로 뻗어나가는 그래프가 됩니다.
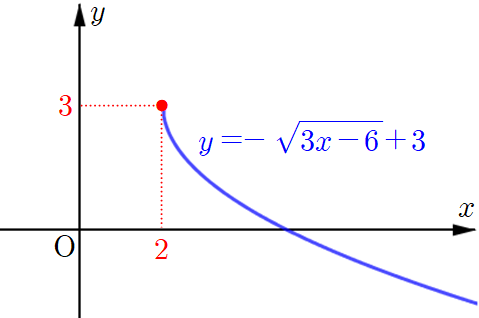
이제 보기를 하나씩 확인해 보면
① 정의역은 $\left\{x~|~x\geq 2 \right\}$이다. 참
② 치역은 $\left\{y~|~y\leq 3 \right\}$이다. 참
③ 그래프는 함수 $y=-\sqrt{3x}$의 그래프를 $x$축의 방향으로 $-2$만큼, $y$축의 방향으로 $3$만큼 평행이동한 것이다. $x$축의 방향으로 $-2$만큼이 아니라 $2$만큼 평행이동한 것이므로 거짓
④ 그래프는 제2사분면, 제3사분면을 지나지 않는다. 참
⑤ 역함수는 $y=\frac{1}{3} x^2-2x+5~(x\leq 3)$이다.
$y=-\sqrt{3x-6}+3$에서
$y-3=-\sqrt{3x-6}$
$y^2-6y+9=3x-6$
$y^2-6y+15=3x~(y\leq 3)$
$x$, $y$를 서로 바꾸고 양변을 3으로 나누어 정리하면
$y=\frac{1}{3} x^2-2x+5~(x\leq 3)$
따라서 ⑤번도 참입니다.
이상으로부터 답은 ③번입니다.

실수 전체의 집합에서 정의된 함수 $f$가
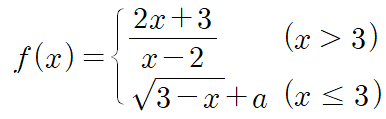
일 때, 함수 $f$는 다음 조건을 만족시킨다.
| (가) 함수 $f$의 치역은 $\left\{y~|~y\geq 2 \right\}$이다. (나) 임의의 두 실수 $x_1$, $x_2$에 대하여 $x_1 \neq x_2$이면 $f(x_1) \neq f(x_2)$ |
$f(2)f(k)=40$일 때, 상수 $k$의 값은? (단, $a$는 상수이다.) [2012/고1/11월학평/4점]
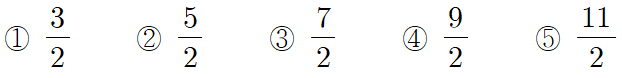
$\frac{2x+3}{x-2}=\frac{7}{x-2}+2$로부터 우선 $x>3$일 때의 유리함수의 그래프를 그리면 다음과 같습니다.
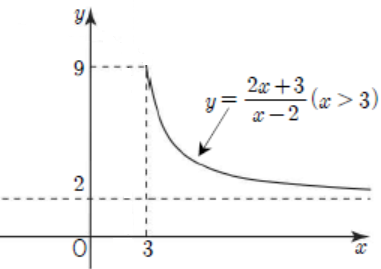
이제 무리함수 $y=\sqrt{3-x}+a$로부터 $x\leq 3$일 때의 그래프를 완성해야 하는데 (가) 조건으로부터 치역이 2보다 큰 모든 실수가 되려면 무리함수의 최솟값이 $9$가 되어야 합니다. 또한, (나) 조건으로부터 일대일함수가 되려면 결국 무리함수의 그래프의 시작점이 다음과 같이 $(3,~9)$가 되어야 함을 알 수 있습니다.
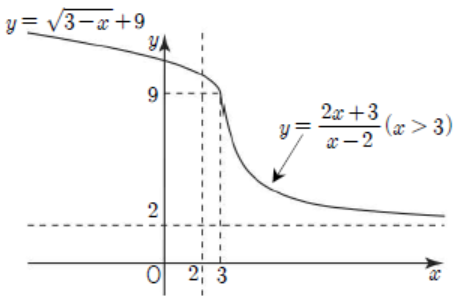
따라서 $f(3)=9$로부터 $a=9$입니다.
따라서
$f(2)=\sqrt{3-2}+9=10$
이고 $f(2)f(k)=10f(k)=40$로부터 $f(k)=4$임을 알 수 있어요.
위의 그래프에서 보다시피 함숫값이 4가 나오려면 $x>3$일 때만 가능하므로 다음과 같이 유리함수에 대입하여 $k$를 찾아냅니다.
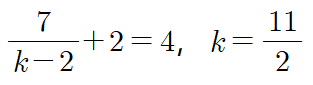
따라서 답은 ⑤번입니다.
♥ 이해가 잘 되셨다면 좋아요와 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 함수' 카테고리의 다른 글
| 수학으로 사랑 고백하는 법 (고1 수학 원의 방정식, 무리함수로 완벽한 하트 그래프 그리기) (5) | 2023.09.18 |
|---|---|
| 무리함수 y=±√ax의 그래프에 대한 자세한 이해 (고1 수학 함수) (0) | 2023.09.08 |
| 무리식, 무리함수에 대한 자세한 이해 (고1 수학 함수) (0) | 2023.08.29 |
| 유리함수의 역함수 구하는 법, 역함수의 특징 (고1 수학 함수 개념) (0) | 2023.02.20 |
| 유리함수 y=(ax+b)/(cx+d)에 대한 자세한 이해 (고1 수학 함수 개념) (7) | 2022.12.15 |





댓글 영역