복소평면에서 드무아브르 정리를 이용하여 복소수(허수)의 거듭제곱 구하기 (고1 수학 방정식과 부등식)

복소평면에서 드무아브르 정리를 이용하여 복소수(허수)의 거듭제곱 구하기 (고1 수학 방정식과 부등식)

바이어슈트라스 타원 함수는 복소수를 변수로 한 함수로 복소평면 위에 투영된 그래프를 그리면 위의 그림과 같이 주기성을 띕니다.

 안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽게 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.

 지난 포스팅에서 복소수를 이용하여 음수의 제곱근을 정의하고 구하는 법을 알아보았습니다.  복소수 단원을 끝내기 전에 복소수와 관련된 문제 중 흔히 출제되는 복소수의 거듭제곱에 대한 얘기를 해보고자 합니다.

 

● 들어가기

 복소수는 대체로 거듭제곱을 하면 간단한 실수가 만들어지는 경향이 있습니다. 특히, 그중에는 거듭제곱을 하여 $1$이 되어 제곱을 할수록 같은 값을 거치며 순환하는 복소수도 많이 존재하죠. 이때 $n$제곱하여 $1$이 되는 $n$의 최솟값을 주기라 할 수 있는데 문제집에서는 이를 활용한 문제를 묻는 경우가 많습니다.

다음 문제를 풀어볼까요?

 

 

---

이렇게 단순히 몇 번 곱하면 그 패턴이 드러나서 답을 구할 수 있는 형태의 문제인데 문제에서 수식을 어떻게 제시하느냐에 따라 꽤나 귀찮은 계산을 해야 할 수도 있죠. 물론 반복적인 계산만으로도 웬만한 문제는 거의 해결할 수 있습니다. 왜냐하면 지금부터 소개하는 내용은 고등학교의 교육과정을 훨씬 뛰어넘는 내용이니까요.

혹시 복소수에서 왜 이런 패턴이 나타나며 이러한 패턴을 보이는 복소수는 어떤 특징을 가지고 있는지 궁금증을 가진 분들이 있다면 오늘 소개하는 내용이 그 해답이 됩니다.

반응형

● 복소평면

 복소수가 실수와 다른 점은 하나의 복소수를 결정하기 위해 실수부분과 허수부분의 두 수가 필요하다고 말한 적이 있었죠. 따라서 지금까지 실수를 표현한 것과 다르게 수직선 위에는 허수를 표현할 수 없고 다음과 같이 좌표평면 위의 점의 좌표를 표현하는 것처럼 평면좌표를 도입해야 합니다.

이때, 가로축은 실수부분, 세로축은 허수부분이 되는데 이런 좌표평면을 복소평면이라고 합니다. 일반적으로 실수 $a$, $b$에 대하여 복소수 $a+bi$의 위치는 그림과 같이 나타냅니다.

예를 들어, 복소평면에서 $3+4i$의 위치는 다음과 같아요.

 

● 복소수의 절댓값

 고등학교 교육과정에서는 소수에 대해서는 절댓값을 정의한 적이 없었지만, 복소수에서도 절댓값을 정의할 수 있습니다. 여러분이 실수에서의 절댓값의 정의를 어떻게 기억하고 계실지는 모르겠지만 절댓값이란 단순히 마이너스를 없애는 개념이 아니고 그 실수에서 원점까지의 거리를 의미해요. 예를 들어 $-5$의 절댓값이 $5$인 이유는 수직선에서 $-5$와 $0$ 사이의 거리가 $5$이기 때문입니다.

 이러한 원리를 확장해서 복소수의 절댓값은 그림과 같이 복소평면에서의 복소수가 나타내는 점과 원점까지의 거리를 의미합니다.

이 거리를 $r$로 놓고 위의 그림에서 가로길이가 $a$, 세로 길이가 $b$인 직각삼각형의 빗변의 길이로서 생각하면 피타고라스 정리에 의해 $r^2=a^2+b^2$이므로 $r=\sqrt{a^2+b^2}$임을 쉽게 알 수 있죠. 즉, 복소수 $z=a+bi$ ($a$, $b$는 실수)의 절댓값은 다음과 같이 정의됩니다.

$|z|=\sqrt{a^2+b^2}$

켤레복소수를 이용하여 표현하면 $|z|=\sqrt{z\bar{z}}$가 됩니다. 예를 들어 복소수의 $4-3i$의 절댓값은 다음의 계산을 통해 $5$임을 구할 수 있어요.

$|4-3i|=\sqrt{4^2+(-3{)}^2}=5$

복소수는 그 자체로는 대소비교를 할 수 없지만, 절댓값의 개념을 이용하면 복소수끼리도 대소비교가 가능해집니다.

 

● 복소수의 편각과 극형식

 이와 같이 복소수를 평면에 표현하면 그로 인해 원점과의 거리로서 절댓값을 정의할 수 있고 그림처럼 원점까지 이은 선분이 가로축인 실수축과 이루는 각 $\theta$ 또한 하나로 결정됩니다.

이 각 $\theta$를 $z=a+bi$의 편각(argument)라 부르며 $\theta =\arg (z)$로 나타냅니다. 물론 이런 전문 기호까지 알 필요는 없으니 여기서는 그냥 편각이라고만 부르겠습니다.

 중요한 것은 원점까지의 거리 $r$과 실수축과의 편각 $\theta$가 정해지면 복소평면 위에서 딱 하나의 고유한 위치가 정해지기 때문에 복소수 $z$가 나타내는 위치를 $(r,\theta )$와 같이 나타낼 수도 있다는 거예요. 즉, 임의의 복소수 $z$는 실수부분과 허수부분를 변수로 하는 대신 $r$과 $\theta$를 변수로 하여 다음과 같이 나타낼 수 있습니다.

$z=r(\cos \theta +i\sin \theta )$

이 식을 복소수의 극형식이라고 합니다. 예를 들어 복소평면에서 허수 $1+\sqrt{3}i$의 위치는 다음 그림에서 표시한 점과 같습니다.

그럼 이 수의 절댓값은 $2$이고 그림의 직각삼각형에서 각 $\theta$의 값은 ${60}^{\circ }$이죠. 따라서 이 수는 극형식으로 다음과 같이 나타낼 수 있어요.

$1+\sqrt{3}i=2(\cos {60}^{\circ }+i\sin {60}^{\circ })$

 

● 드무아브르 정리

 이제 오늘의 강의에서 소개할 개념의 종착지까지 왔습니다. 위에서 복소수의 극형식에 대해 알아봤는데 여기서 특별히 $|z|=r=1$이 되면 오직 편각 $\theta$만으로 복소수를 표현할 수 있게 되죠. 이때 다음의 성질이 성립하는데 이게 바로 드무아브르의 정리(De Moivre's theorem)입니다.

$(\cos \theta +i\sin \theta {)}^n=\cos (n\theta )+i\sin (n\theta )$

 이 놀라운 정리는 이름 그대로 프랑스 출신의 영국 수학자 드무아브르(1667~1754)가 만든 것으로 일반적으로 $n$이 유리수일 때 성립하지만, 편의상 자연수로 생각하고 기억하시면 돼요. 이 정리는 고등학교 교육과정의 수준을 한참 벗어나지만 $n$을 자연수로 한정하면 고등학교의 미적분 과목에서 등장하는 삼각함수의 배각 공식과 2학년 과정인 수학적 귀납법을 이용하여 증명이 가능합니다. 고1 수준에서는 이 정리의 증명을 할 수는 없지만, 이 공식을 잘 써먹을 수 있으면 복소수의 거듭제곱에서 매우 강력한 힘을 발휘할 수 있습니다.

예를 들어 복소수 $z=\frac{1+i}{\sqrt{2}}$의 절댓값을 구하면 $\frac{1^2+1^2}{2}=1$이죠. 이제 이 수를 거듭제곱하면 다음과 같습니다.

그리고 이 값들을 복소평면에 나타내면 다음 그림과 같습니다.

보다시피 처음 $z$와 이 수를 거듭제곱한 수들의 절댓값은 모두 $1$임을 알 수 있습니다. 그리고 $z$의 편각은 ${45}^{\circ }$이고 $z^2$의 편각은 ${90}^{\circ }$, $z^3$의 편각은 ${135}^{\circ }$, 이렇게 제곱을 거듭할수록 편각은 ${45}^{\circ }$씩 증가합니다. 즉, $z$를 $n$제곱하였더니 $z$의 편각은 $n$배가 되고 있죠. 이러한 규칙에 의해 거듭제곱을 계속하면 $z^8=1$이 됨을 알 수 있습니다.

 

● 활용 문제 풀이

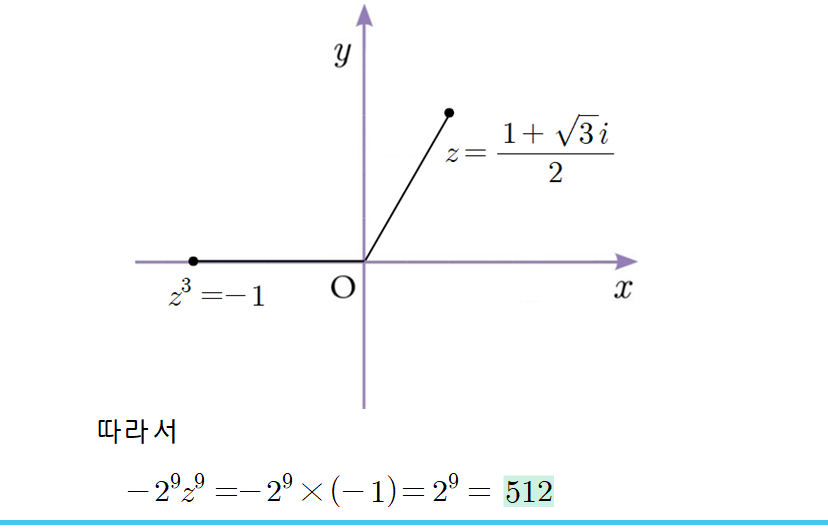
위에서 풀었던 예제1을 배운 내용으로 다시 풀어보겠습니다.

---

 

이와 같이 드무아브르의 정리를 활용하면 절댓값이 1인 복소수의 거듭제곱을 계산하는데 매우 유용합니다. 또한, 절댓값이 1이 아니더라도 식을 적절히 변형한 다음 편각을 $n$배 하는 방법으로 거듭제곱을 구할 수 있습니다.

 

---

 

♥ 이해가 잘 되셨다면 좋아요와 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.