고정 헤더 영역
상세 컨텐츠
본문
복소수의 사칙연산 및 켤레복소수에 대한 자세한 이해 (고1 수학 방정식과 부등식, 기출문제 풀이 포함)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
지난 포스팅에서 허수와 복소수에 대해서 알아봤는데요. 오늘은 새롭게 배운 복소수로 간단하게 사칙연산하는 방법과 켤레복소수에 대해 알아보도록 하겠습니다.

● 켤레복소수
이미지에서 보셨듯이 '켤레'란 서로 짝이 되는 대상을 지칭하는 단어로 외래어이긴 하나 옛날부터 쓰던 말입니다. 복소수에서도 서로 한 쌍을 이루는 복소수가 존재하는데요. 켤레복소수는 다음과 같이 정의합니다.
| ■ 켤레복소수 |
| 복소수 $z=a+bi$ ($a$, $b$는 실수) 에 대하여 허수부분의 부호를 바꾼 복소수 $a-bi$를 $a+bi$의 켤레복소수라고 하며 기호로 $\overline{z}= \overline{a+bi}$와 같이 나타낸다. |
즉, $\overline{a+bi}=a-bi$입니다. 또한, $a-bi$에서 허수부분의 부호를 또 바꾸면 $a-(-bi)=a+bi$가 되므로 $a+bi$와 $a-bi$는 서로가 켤레복소수와 되어 한 세트를 이룹니다. 켤레복소수는 서로가 한 짝이 되어 연산에서 중요한 역할을 합니다. $\overline{z}$를 읽을 때는 편하게 ‘$z$ 바’라고 읽으면 됩니다.

● 복소수의 덧셈, 뺄셈, 곱셈
수체계를 확장하였으니 이제부터는 확장된 수로 사칙연산을 해볼 거예요. 물론 지금까지 공부했던 수의 사칙연산에서 기본원칙은 바뀌지 않으며, 새로 배운 $i$를 추가해서 계산을 할 것이므로 $i$를 문자처럼 생각하여 계산하되, $i$의 거듭제곱이 있으면 $i^2=-1$임을 이용하여 풉니다.
아래에 정리된 내용은 공식처럼 외우는 것이 아니라 덧셈, 뺄셈, 곱셈을 하는 요령으로 기억하시면 됩니다.

덧셈과 뺄셈은 간단하게 실수는 실수끼리, 허수는 허수끼리 동류항으로 취급하여 계산하면 돼요. 그리고 곱셈은 다음의 간단한 유도과정을 거칩니다.
$(a+bi)(c+di)=ac+(ad+bc)i+bdi^2$
$=ac+(ad+bc)i-bd=(ac-bd)+(ad+bc)i$
다음 내용을 통해 예시와 요령을 익혀보세요.

추가로 허수단위 $i$의 거듭제곱을 정리해 보면
$i^2=-1$, $i^3=-i$, $i^4=-i^2=1$
이므로 네제곱을 하면 $1$이 되죠. 따라서 자연수 $n$, $a$에 대하여 다음이 성립함을 알 수 있어요.
$i^{4n+a}=i^a$


● 연산을 통해 본 켤레복소수의 성질
위의 문제에서 $a$, $b$가 실수일 때, $(a+bi)(a-bi)$의 계산은 $a^2+b^2$으로 일반화할 수 있습니다. 또한, $(a+bi)+(a-bi)=2a$이므로 켤레복소수끼리의 연산은 덧셈이나 곱셈 모두 실수를 만든다는 것을 알 수 있습니다.
그럼 반대로 생각해서 덧셈과 곱셈을 했을 때 모두 실수가 되는 두 수는 서로 어떤 관계를 가지고 있을까요? 다음의 유도과정을 통해 서로 켤레복소수가 됨을 알 수 있어요.

$z_1$과 $z_2$를 임의의 두 허수로 가정했는데 계산과정을 통해 $z_2$가 $z_1$의 켤레복소수가 됨을 확인했죠. 이상으로부터 합과 곱이 모두 실수가 되는 두 허수의 관계는 켤레복소수가 유일함을 알 수 있습니다.

● 순허수
$2i$, $-\sqrt{3}i$와 같이 실수부분이 $0$인 허수를 ‘순허수’라고 합니다. 순허수라는 용어는 교과서에는 소개되어있지 않으나 제곱을 하면 음수인 실수가 되므로 복소수 계산에 유용한 의미를 가집니다.
실제로 복소수 $z=a+bi$에 대하여 $z^2$이 음수이면
$z^2=(a^2-b^2)+2abi<0$
$a^2-b^2<0$ 이고 $ab=0$
위의 두 조건을 만족하려면 $a^2<b^2$인 동시에 $a$ 또는 $b$가 $0$이 되어야 하므로 $a=0$이고 $b\neq 0$가 될 수밖에 없죠. 즉, $z$는 순허수가 됩니다.
이상으로부터 제곱하여 음수가 되는 복소수는 반드시 순허수라는 것을 알 수 있습니다.
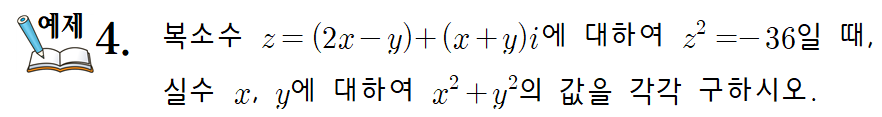
● 복소수의 나눗셈
이제 복소수의 나눗셈이 남았는데 복소수의 나눗셈은 분모에 복소수가 들어가는 경우를 말합니다. 우리는 중3 때 무리수의 나눗셈을 하면서 분모에 근호가 포함된 수는 계산이 덜 된 것으로 간주하여 다음과 같이 분모의 유리화를 시켜서 계산한 바 있습니다.
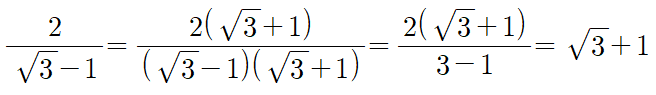
마찬가지로 분모에 허수가 있으면 분모를 실수화 하여 계산하는 것이 복소수의 나눗셈입니다. 그럼 분모를 실수로 만들려면 분모, 분자에 어떤 수를 곱하면 될까요? 바로 켤레복소수입니다. 다음 내용 역시 공식처럼 외울 게 아니라 요령을 기억하시면 됩니다.


마지막으로 기출문제를 통해 응용력을 키워봅시다.

♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.
'고1 수학의 남다른 개념 > 방정식과 부등식' 카테고리의 다른 글
| 이차방정식의 근과 판별식에 대한 자세한 이해 (고1 수학 방정식과 부등식) (0) | 2024.03.24 |
|---|---|
| 복소평면에서 드무아브르 정리를 이용하여 복소수(허수)의 거듭제곱 구하기 (고1 수학 방정식과 부등식) (2) | 2024.03.17 |
| 음수의 제곱근 및 그 기본 성질에 대한 자세한 이해 (고1 수학 방정식과 부등식) (2) | 2024.03.03 |
| 켤레복소수에서 필수로 알아야 할 사칙연산에 대한 기본 성질 (고1 수학 방정식과 부등식) (2) | 2024.02.27 |
| 허수 단위 i 및 복소수의 뜻과 도입 배경 (고1 수학 방정식과 부등식) (4) | 2024.02.18 |










댓글 영역