고정 헤더 영역
상세 컨텐츠
본문

명제와 조건, 진리집합에 대한 자세한 이해 (고1수학 집합과 명제)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
오늘부터는 명제에 대한 강의를 시작하겠습니다. 집합은 수학적 개념과 대상을 조직화, 체계화 하는데 필수적인 개념이죠. 명제 또한 수학에서 근본적으로 사용하는 언어이므로 반드시 공부가 필요한 단원입니다. 국어에서도 논리를 위해 명제가 쓰일 만큼 중요한 개념이죠. 이 집합과 명제가 하나의 대단원 안에 묶여있는 이유는 이 둘이 밀접한 관련이 있기 때문이고 공통된 특징이 있기 때문입니다. 그 공통된 특징은 바로 분명한 기준입니다.

● 명제의 개념
집합은 기준이 분명한 대상들의 모임으로 정했죠. 이와 비슷하게 참 또는 거짓을 명확하게 판별할 수 있는 문장이나 식을 명제라고 합니다. 반대로 참인지 거짓인지 기준이 명확하지 않은 문장은 명제가 아니죠.
따라서 다음과 같은 문장은 모두 명제가 됩니다.
| 15는 3의 배수이다. (참) 1+1=3 (거짓) 사람은 곤충이다. (거짓) 한라산은 백두산보다 높다. (거짓) 정삼각형의 세 내각의 크기는 모두 같다. (참) |
반면, 다음과 같이 참인지 거짓인지 분명하지 않은 문장은 명제가 아닙니다.
15는 아름다운 수이다. 한라산은 높은 산이다. 대한민국은 부유한 나라이다. 저것 좀 치워라. 당신을 사랑합니다. 마음이 아픕니다. 다음을 계산하시오. |
수학에서 전개되는 내용은 거의 대부분이 명제로 이루어졌다고 볼 수 있죠. 교과서나 문제집에서 네모 박스 안에 정리된 개념이 전부 명제라고 보시면 됩니다. 그만큼 명제는 수학에서 숫자만큼이나 큰 비중을 차지합니다.
명제는 영어로 proposition이며 명제를 문장이 아니라 문자로 축약해서 나타낼 때는 보통 알파벳 소문자
| p: 15는 3의 배수이다. q: 1+1=3 일 때, p는 참이고 q는 거짓이다. |
위에서 p와 q는 각각 명제이죠. 또한, 네모박스 안의 문장 전체가 참이므로 이 또한 하나의 명제로 볼 수도 있습니다.
● 조건의 개념
위의 예시에서
참고로, 변수
그렇다면 이렇게 조건이 정의되면 우리의 관심사는 뭐가 될까요? 바로 조건을 만족시키는 대상이 되겠죠? 전체집합
예를 들어, 조건 '
다음 추가적인 예시를 통해 조건과 진리집합의 개념을 익힐 수 있습니다.


전체집합
의 진리집합을 각각
①
따라서
● 명제 p →q의 참, 거짓
그렇다면 명제와 조건은 서로 어떤 관계가 있을까요? 조건은 그 자체로는 명제가 되지 않지만 변수에 구체적인 값을 대입하면 명제가 된다고 배웠죠. 비슷하게 변수에다가 구체적인 조건을 부여해도 명제가 됩니다. 즉, 다음과 같이 조건과 조건을 가정과 결론으로 연결하면 명제가 됩니다.
위의 문장은 위에서 알아본 두 조건 '
| 명제 | 가정 | 결론 |
| 15는 3의 배수이다. | ||
| 1+1=3 | ||
| 정삼각형의 세 내각의 크기는 모두 같다. |
이렇게 변수가 들어있지 않는 명제도 가정과 결론으로 쪼개면 변수가 생성된다는 것을 알 수 있죠. 따라서 조건 또한 사용된 문자만 일치하면 어떠한 두 조건이든 가정과 결론으로 연결하면 명제가 됩니다. 즉, 조건은 명제를 만드는 재료가 되는 거죠.
이와 같이 두 조건
와 같이 나타냅니다.
예를 들어 두 조건
으로 나타낼 수 있습니다.
그렇다면 이 명제는 참일까요, 거짓일까요? 이 정도의 명제는 직관적으로도 거짓이라는 걸 금방 판별할 수 있죠? 왜냐하면
단, 두 조건을 서로 바꿔서
그렇다면 이런 명제의 참, 거짓을 판단하는 기준에는 어떤 원리가 들어있을까요? 그것은 바로 각 조건의 진리집합에 있습니다. 이 진리집합간의 포함관계를 통해 명제의 참, 거짓을 판별할 수 있습니다.
명제
따라서 명제
| ■ 명제 |
| ① ② |
위의 예시를 다시 들면, 명제 '
또한, 명제 '
반대로 두 집합

실수
①
으로부터 조건
또한,
명제
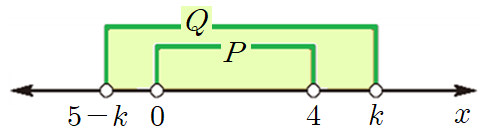
따라서
따라서
♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 집합과 명제' 카테고리의 다른 글
| ‘모든’이나 ‘어떤’이 있는 명제에 대한 자세한 이해 (고1수학 집합과 명제) (6) | 2022.08.20 |
|---|---|
| 명제와 조건의 부정 및 '그리고'와 '또는'의 관계 (고1수학 집합과 명제) (8) | 2022.08.18 |
| 집합의 활용 - 각종 문제 유형 탐색 및 풀이 (고1수학 집합과 명제) (5) | 2022.08.10 |
| 집합의 활용 - 수 체계의 집합 표현 및 포함 관계 (고1수학 집합과 명제) (6) | 2022.08.06 |
| 집합의 연산 - 드모르간의 법칙에 대한 쉽고 자세한 이해 (고1수학 집합과 명제) (0) | 2022.08.02 |





댓글 영역