고정 헤더 영역
상세 컨텐츠
본문
두 함수가 같을 조건, 함수의 그래프에 대한 자세한 이해 (고1수학 함수)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
함수 단원의 두 번째 강의입니다. 지난 강의에서 집합을 이용하여 함수를 재정의했는데요. 오늘은 이어서 두 함수가 같을 조건과 함수의 그래프에 대해 알아보겠습니다.

● 두 함수가 같을 조건
수학에서 새로운 대상을 정의하면 두 대상이 같을 조건도 정의를 해줘야겠지요. 집합의 경우는 두 집합이 같을 조건은 서로가 서로의 부분집합이 되는 것이었습니다. 함수의 경우도 두 함수가 같으려면 하나의 함수를 복사, 붙여 넣기 한 것처럼 모든 것이 일치해야만 하죠. 따라서 다음과 같이 정의됩니다.
| 두 함수 $f$, $g$에 대하여 정의역과 공역이 각각 같고 정의역의 모든 원소 $x$에 대하여 $f(x)=g(x)$일 때, 두 함수 $f$와 $g$는 서로 같다고 하며, 이것을 기호로 $f=g$와 같이 나타낸다. |
같다는 것을 나타내기 위해 역시 등호($=$) 기호를 사용하죠. 반면, 두 함수가 서로 같지 않을 때에는 $f\neq g$와 같이 표현합니다. 여기서 정의역과 공역이 '각각' 같다는 말은 (정의역)$=$(공역)이란 뜻이 아니라 두 함수의 정의역끼리 같고, 공역끼리 같다는 뜻이에요.
이 정의에 의하면 두 함수가 같으려면 $f(x)=g(x)$만 성립해야 하는 것이 아니라 대응 관계를 이루는 두 집합 역시 똑같아야 한다는 것을 보여줍니다.
예를 들어, 두 함수 $f$, $g$에 대하여 $f(x)=g(x)=x+1$로 수식이 똑같이 주어졌다 해도 $f$의 정의역이 $\left\{1,~2\right\}$이고 $g$의 정의역이 $\left\{2,~3\right\}$이면 다음과 같이 두 함수는 완전히 다른 대응관계를 보입니다.

또한, 두 함수 $f$, $g$에 대하여 $f(x)=x-1$, $g(x)=x^2-1$로 두 함수의 수식이 다르게 지정된 경우에도 두 함수의 정의역이 $\left\{0,~1\right\}$이라면
$f(0)=g(0)=-1$, $f(1)=g(1)=0$
이 되어 두 함수가 일치할 조건을 만족하므로 $f=g$입니다. 참고로 두 함수의 공역은 따로 언급하지 않았으므로 둘 다 실수 전체 집합인 것으로 생각하여 공역 또한 일치한다고 할 수 있습니다.
이처럼 수식이 같은 경우에도 두 함수는 다를 수도 있고, 수식이 다른 경우에도 두 함수는 같을 수도 있습니다. 따라서 이제부터는 함수가 수식에 의해서만 결정된다는 편견을 깨야하는 거죠.

두 집합 $X=\left\{0,~1,~2\right\}$, $Y=\left\{1,~2,~3,~4\right\}$에 대하여 두 함수 $f:X~$→$~Y$, $g:X~$→$~Y$를 $f(x)=2x^2-4x+3$, $g(x)=a|x-1|+b$라 하자.
두 함수 $f$와 $g$가 서로 같도록 하는 상수 $a$, $b$에 대하여 $2a-b$의 값은? [2013.11/3점]
① $-3$ ② $-1$ ③ $1$ ④ $3$ ⑤ $5$
정의역과 공역은 이미 정해졌으므로 다음이 성립하면 됩니다.
$f(0)=g(0)$, $f(1)=g(1)$, $f(2)=g(2)$
먼저 $f(1)=g(1)$부터 대입하면 미지수 $b$는 바로 알 수 있어요.
$f(1)=1$, $g(1)=b$, $b=1$
이제 하나만 더 비교해보면 되므로 $f(0)=g(0)$을 대입하면
$f(0)=3$, $g(0)=a+b=a+1$, $a=2$
따라서 $2a-b=4-1=3$이므로 답은 ④번입니다.
● 함수의 그래프
함수의 그래프 또한 이미 알고 있는 내용이나 함수 자체를 다시 정의했으므로 함수의 그래프 또한 다음과 같이 새롭게 정의합니다.
| 함수 $f:X~$→$~Y$에서 정의역 $X$의 원소 $x$와 이에 대응하는 함숫값 $f(x)$의 순서쌍 $(x,~f(x))$ 전체의 집합 $\left\{(x,~f(x))~|~x\in X\right\}$를 함수 의 그래프라고 한다. |
즉, 함수의 그래프 또한 집합으로 정의하고 있는 것을 알 수 있죠. 일반적으로 도형은 점들이 모여서 만들어진 것이므로 도형은 집합의 일종이에요. 함수의 그래프는 도형의 일종이므로 이 또한 집합으로 정의됩니다.
다음의 두 가지 예시를 들 수 있습니다.

지금까지 우리가 배웠던 함수의 그래프가 직선, 포물선 등이 있었는데 이것들이 모두 실선이었던 이유는 뭘까요? 지금까지 배웠던 함수들은 모두 정의역을 실수 전체의 집합으로 기본 전제를 깔았기 때문입니다. 실수 전체의 집합 안에서 점 $(x,~f(x))$가 무수히 많이 찍히면서 그것이 실선을 이루는 것이죠. 따라서 이제부터는 함수의 그래프는 실선으로 그려질 것이라는 편견 또한 깨야하는 겁니다. 함수의 그래프는 점을 찍는 것으로 시작됩니다.
함수는 각 $x$의 값에 집합 $Y$의 원소가 하나씩만 대응해야 하므로 정의역의 원소 $a$에 대하여 그림과 같이 $x$축에 수직인 직선 $x=a$를 그어보면 어디에서든 교점이 하나씩만 나오는 것이 특징입니다.
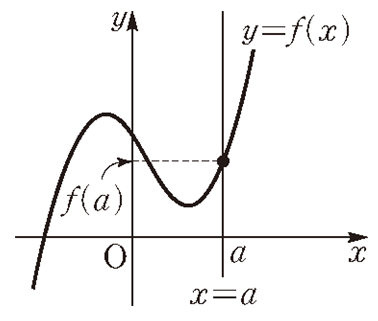
만약 교점이 두 개 이상 나오는 곳이 하나라도 있으면 그 그래프는 함수의 그래프가 될 수 없습니다. 예를 들어, 직선이나 포물선은 일치함수, 이차함수로 각각 표현되지만 원의 방정식은 '방정식'으로만 배웠지 함수를 배운 적은 없죠. 원은 다음과 같이 $x$축에 수직인 직선에 대하여 교점이 2개씩 나오는 구간이 존재하기 때문입니다. 이것은 하나의 $x$값에 대하여 두 개의 $y$값이 대응하는 것이므로 함수의 조건을 만족하지 않습니다.
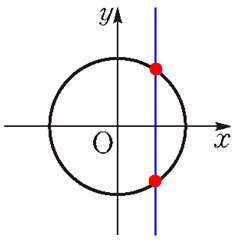
추가로 서로 같은 두 함수가 있다면 그 함수의 그래프 또한 일치하겠죠. 따라서 두 함수의 일치여부는 그래프의 일치 여부를 통해 확인할 수도 있습니다.
● 함수의 그래프 - 심화
내신 대비를 위한 공부라면 여기까지만 하셔도 됩니다. 지금부터는 함수의 그래프에 대해서 교육과정에서는 다루지 않는 좀 더 심화된 내용을 얘기해 볼 건데 다음 그래프를 한 번 볼까요? 이 그래프는 함수의 그래프가 될 수 있을까요, 없을까요?

$x$축과 수직인 직선이 그래프와 만나는 점이 두 개니까 당연히 함수가 될 수 없는 거 아닌가? 하고 생각하시겠죠.
그렇다면 다음 함수의 그래프는 어떻게 그려질까요?

유리수 집합과 무리수 집합은 서로소이므로 이렇게 대응하면 각 $x$에 대하여 $f(x)$의 값은 $1$과 $2$중 딱 하나의 값이 정해집니다. 그리고 이 함수의 그래프는 다음 그림과 가깝게 그려집니다.

이 그림을 보면 누군가는 이 함수의 그래프는 하나의 직선으로 연결되어 있지 않으므로 실선이 아니라 점선으로 그려야 하지 않냐고 주장할 수 있습니다. 그러나 $\cdots\cdots \cdots $와 같이 점선으로 그리면 아무리 점을 촘촘히 빼곡하게 찍어도 그걸 확대하면 빈 공간이 생기기 마련이죠. 무리수와 유리수는 조밀하게 구성된 집합이라 빈 점이 있을 수는 있어도 빈 공간이 존재할 수는 없습니다.
이미 우리는 무리수의 존재를 모르고 유리수 집합을 수 전체의 집합으로 생각했던 중학교 1학년 때 정비례 함수를 배웠을 때도 그 그래프는 (실)직선으로 그렸지 점선으로 그리지는 않았죠. 따라서 실선과 점선 중 하나를 택해서 그려야 한다면 실선으로 그리는 것이 실제 함수에 가깝다고 볼 수 있습니다.
따라서 직선이 두 개 그어진 것처럼 보이는 그래프도 함수의 그래프가 될 수 있는 거죠. 같은 예로 원 모양처럼 그린 그래프도 다음과 같이 함수를 정의하면 함수의 그래프가 됩니다.

이 함수를 $y=\pm \sqrt{1-x^2}$로 놓고 양변을 제곱하여 정리하면
$y^2=1-x^2$, $x^2+y^2=1$
이 되어 원의 방정식을 이룹니다. 따라서 이 함수의 그래프는 다음과 같이 $x$가 유리수일 때는 $x$축 위에 그려지고 $x$가 무리수일 때는 $x$축 아래에 그려집니다.

물론 위에서 제시한 두 함수는 완벽하게 직선이나 원을 그리지 못합니다. 그냥 직선이나 원에 가깝게 그려지는 것일 뿐이죠.
집합을 공부할 때 벤다이어그램은 집합을 가시적으로 표현하는 도구라서 엄밀한 증명에 이용할 수는 없다는 말을 한 적이 있었죠. 함수의 그래프도 마찬가지입니다. 함수의 그래프 또한 함수를 가시적으로 이해하기 위한 도구일 뿐이지, 수학에서 엄밀한 증명을 하는데 쓰일 수는 없는데, 그 이유가 바로 여기에 있는 거예요. 보다시피 그림을 통한 그래프로는 함수를 완벽하게 표현할 수 없기 때문입니다.
이 포스팅 대표 이미지로 사용된 다음의 그래프를 나타내는 함수를 '토마에 함수(Thomae's function)'라고 부르는데 이 함수는 다음과 같이 정의됩니다.


이 함수의 그래프는 $x$축에 가까울수록 점이 무수히 많아지는 모양을 이루는데 그 값이 워낙 복잡하게 구성되어 있어서 이를 그림을 통해 $x$축 근방의 그래프를 완벽하게 구현하는 것은 불가능합니다. 이렇듯 수학에서 연구하는 함수는 그래프만으로는 표현이 곤란한 함수들이 많이 존재합니다.
따라서 학교 선생님 중에서 이 포스팅을 보고 계신 분이 계신다면 함수의 그래프와 관련된 문제를 내실 때는 신중하실 필요가 있습니다. 막연하게 "다음 중 함수의 그래프가 아닌 것은?"이라고 묻는다면 정답으로 의도한 그래프도 제가 보여드린 예시와 같이 그 그래프를 나타내는 함수를 만들 수 있기 때문이에요.
따라서 시험 문제를 내실 때 그래프와 같은 그림을 제시한다면 반드시 그 그래프가 어떻게 그려진 그래프인지 구체적인 설명을 달아주셔야 합니다. 도형 문제를 내실 때도 마찬가지고요.
오늘 포스팅은 여기까지입니다. 함수 개념을 이해하는데 도움이 되셨길 바라며 즐거운 저녁 보내세요!
♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 함수' 카테고리의 다른 글
| 사다리 타기 게임의 자세한 원리 - 일대일대응의 합성 (고1수학 함수) (4) | 2022.09.30 |
|---|---|
| 합성함수의 기본성질(교환법칙, 결합법칙)에 대한 자세한 이해 (고1수학 함수) (0) | 2022.09.28 |
| 합성함수의 개념에 대한 자세한 이해 (고1수학 함수) (2) | 2022.09.24 |
| 일대일함수, 일대일대응, 항등함수, 상수함수의 자세한 이해 (고1수학 함수) (14) | 2022.09.20 |
| 함수의 뜻, 정의, 개념에 대한 자세한 이해 (고1수학 함수) (10) | 2022.09.13 |





댓글 영역