고정 헤더 영역
상세 컨텐츠
본문

대칭이동의 활용 - 최단 거리&길이의 최솟값 구하기 (고1수학 도형의 방정식)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
지금까지 몇 개의 포스팅을 통해 다양한 대칭이동을 하는 원리를 알아보았습니다. 이 포스팅에서는 대칭이동을 활용하여 주어진 상황에서 최단거리를 구하는 문제를 풀어보려고 합니다. 최단거리 문제는 대칭이동을 활용한 대표적인 유형이라 할 수 있으며 시험에서도 필수로 출제되는 문제이니 확실히 익혀두시기 바랍니다.

● 기본 원리
최단거리를 구하는 기본 원리는 다음과 같이 교과서에 자세히 소개되어 있습니다. (출처: 좋은책 신사고 수학)
 |
즉, 직선 위를 움직이는 점이 있으면 그 직선을 대칭축으로 하여 대칭이동을 해보면 모든 최단거리 문제를 해결할 수 있습니다.
예를 들어, 다음 그림과 같이 두 점

핵심 원리는 다음 그림과 같이 점

그러면
이때,
● 연습 문제 풀이

다음 그림과 같이 가로, 세로의 길이가 각각 2m, 1m인 직사각형 모양의 당구대 ABCD가 있다. 변 BC에서 0.5m, 변 CD에서 0.4m 떨어진 지점에 있는 당구공이 변 BC와 변 AB에 차례대로 한 번씩 부딪힌 다음 D지점의 구멍으로 들어갔을 때, 당구공이 움직인 거리를 구하시오. (단, 공과 구멍의 크기는 무시하고, 공이 변에 부딪힐 때의 입사각과 반사각의 크기는 같다.) [좋은책 신사고 수학]

위에서 제시한 교과서 자료의 해당 페이지에 같이 있는 문제입니다. 이 문제는 최단거리를 묻는 것이 아니라 반사되어 만들어진 경로의 총길이를 묻고 있죠. 그러나 대칭이동의 원리는 똑같습니다.
다음 그림에서 흰색으로 표시한 경로가 바로 구하고자 하는 경로입니다. 따라서 당구공이 있는 지점을 직선 BC에 대하여 대칭이동한 후 이 점을 다시 직선 AB에 대하여 대칭이동한 점을 P라 하면 두 점 P, D 사이의 거리가 바로 흰색 경로의 총길이가 됩니다. 대칭이동을 했다고 해서 꺾인 선이 하나의 선분이 되는 이유는 입사각과 반사각이 같기 때문이죠. 따라서 대칭이동 할 때 각도도 이동하면서 맞꼭지각이 같아지는 원리로 인해 하나의 선분으로 연결시켜줍니다.

따라서
그런데 막상 계산하려고 보니까 좀 짜증이 나죠. 이럴 때는 다음과 같이 가로, 세로의 비를 이용하여 계산을 줄일 수 있습니다. 가로의 길이가 3.6, 세로의 길이가 1.5이면 이들의 비는

그런데 가로의 길이가

좌표평면 위에 세 점
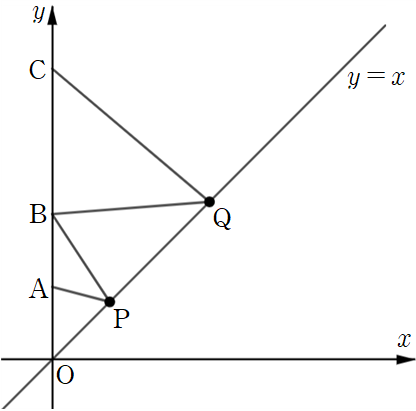
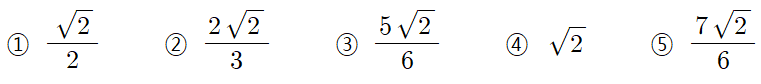
문제에서 세 점
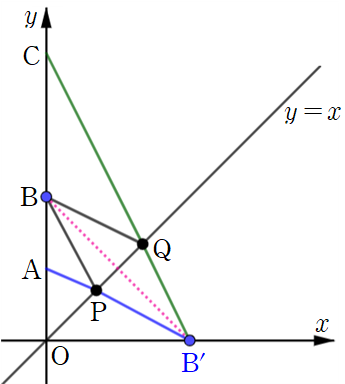
따라서 대칭이동한 점을
이제 점
직선
점
직선
점
따라서 선분
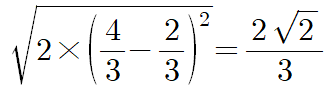
따라서 답은 ②번입니다.

그림과 같이 반지름의 길이가

움직이는 점이 3개나 있어서 어떻게 접근해야 할지 막막할 수도 있겠으나, 부채꼴에서 직선은 두 개뿐이므로 이 직선들에 대하여 대칭이동을 시도해보겠습니다. 즉, 점
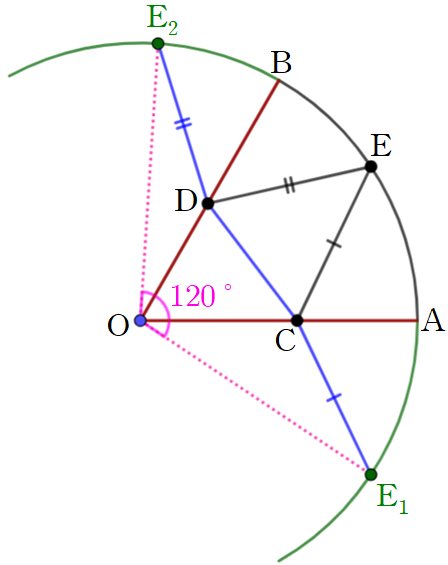
따라서 삼각형 CDE의 둘레의 길이의 최솟값은
이제 이 값을 구하기 위해서 중심각
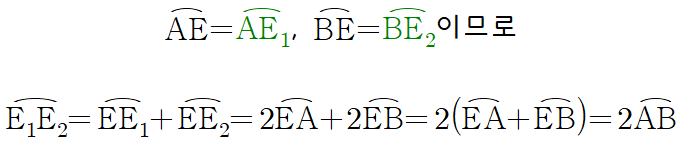
따라서
따라서 선분
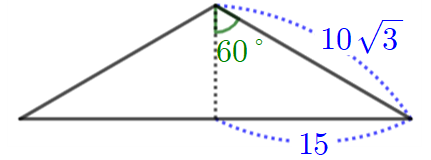
따라서 구하는 길이의 절반이
♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 도형의 방정식' 카테고리의 다른 글
| 대칭이동 심화 - 임의의 직선에 대한 대칭이동 (고1수학 도형의 방정식) (0) | 2022.07.21 |
|---|---|
| 함수 그래프의 대칭 조건에 대한 자세한 이해 (고1수학 도형의 방정식) (2) | 2022.07.18 |
| 도형의 대칭이동 심화 : x=p, y=q, (p, q), y=-x에 대한 대칭이동 (고1수학 도형의 방정식) (0) | 2022.07.18 |
| 대칭이동의 기본 원리 및 x축, y축, 원점, y=x에 대한 대칭이동 (고1수학 도형의 방정식) (2) | 2022.07.13 |
| 왜 뺄셈인가, 도형의 평행이동 원리의 확실한 이해 (고1수학 도형의 방정식) (0) | 2022.07.07 |





댓글 영역