눈꽃송이의 입자는 중심점에 대하여 대칭을 이룹니다. (그림 출처: https://pixabay.com/illustrations/background-pattern-winter-5841885/)
안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다.수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
지난 포스팅에서x축, y축, 원점,y=x에 대한 기본 대칭이동을 알아봤습니다. 그리고 교육과정에서 시험문제로 출제하도록 공식적으로 허용되는 범위도 여기까지입니다. 그러나 안타깝게도 현실은 그렇지가 않죠. 간혹 이 4가지 말고도 다른 점이나 직선에 대하여 대칭을 이루는 원리를 묻는 문제도 종종 등장합니다. 여기서는 직선 $x=p$, 직선 $y=q$, 점 $(p, q)$, 직선 $y=-x$에 대한 대칭이동에 대해 알아보겠습니다.
● 직선 x=p, y=q와 점 (p, q)에 대한 대칭이동
직전 포스팅에서 $x$축, $y$축 및 원점에 대하여 대칭이동한 점의 좌표를다음과 같이 알아보았습니다.
자료 출처: EBS 수학의 왕도 수학 상
여기에서 $x$축, $y$축을 위치만 옮긴 임의의 직선 $x=p$, $y=q$로 놓고 점 $(a,~b)$를 대칭이동 시켜보면 다음과 같습니다. 여기서 $y=q$에 대하여 대칭이동한 점을$(a_1,~b_1)$,$x=p$에 대하여 대칭이동한 점을$(a_2,~b_2)$로 나타내었습니다.
먼저$(a_1,~b_1)$와 $(a,~b)$의 관계를 관찰해보면 두 점을 연결한 선분은 $y=q$와 수직이므로 $a_1=a$입니다. 즉, $x$좌표는 변화가 없죠. 그리고 $y=q$ 위의 점$(a,~q)$는 이 선분의 중점이므로 다음이 성립합니다.
$\frac{b+b_1}{2}=q$ 즉,$b+b_1=2q$ 이고 $b_{1}=2q-b$
마찬가지로$(a_2,~b_2)$와$(a,~b)$의 관계를 관찰해보면 두 점을 연결한 선분은$x=p$와 수직이므로 $b_2=b$가 되어 $y$좌표에는 변화가 없습니다. 그리고$x=p$ 위의 점$(p,~b)$는 이 선분의 중점이므로 다음이 성립합니다.
$\frac{a+a_2}{2}=p$ 즉,$a+a_2=2p$ 이고 $a_2=2p-a$
이 결과는 다음 그림으로 요약할 수 있습니다.
이제 점 $(p,~q)$에 대한 대칭이동까지 알아보겠습니다. 직전 포스팅에서 원점에 대한 대칭이동은 $x$축 대칭이동과 $y$축 대칭이동을 둘 다 한 것과 같다는 것을 배웠죠. 마찬가지로 점 $(p,~q)$에 대한 대칭이동은 직선 $x=p$와 직선 $y=q$에 대한 대칭이동을 둘 다 한 것으로 볼 수 있습니다.
따라서 위 그림과 같이 점 $(a,~b)$를 점 $(p,~q)$에 대하여 대칭이동한 점의 좌표를 $(a',~b')$로 놓으면 다음이 성립합니다.
$\frac{a+a'}{2}=p$ 즉, $a+a'=2p$ 이고 $a'=2p-a$
$\frac{b+b'}{2}=q$ 즉, $b+b'=2q$ 이고 $b'=2q-b$
이상을 정리하면 다음과 같습니다.
예를 들어,점$(5,~3)$을
직선$x=3$에 대하여 대칭이동한 점의 좌표는 $(2\times3-5,~3)=(1,~3)$
직선$y=2$에 대하여 대칭이동한 점의 좌표는 $(5,~2\times2-3)=(5,~1)$
점 $(3,~2)$에대하여 대칭이동한점의 좌표는 $(2\times3-5,~2\times2-3)=(1,~1)$
이고 이 결과는 다음 그림과 같습니다.
반응형
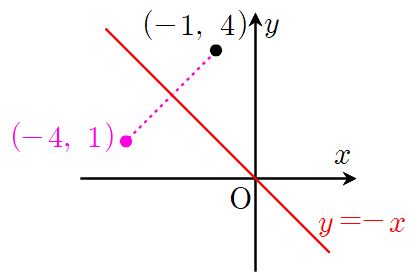
● 직선 y=-x에 대한 점의 대칭이동
직전 포스팅에서는 직선 $y=x$에 대한 대칭이동을 알아봤습니다. 그러나 이 직선과 수직을 이루는 쌍둥이 직선이 하나 더 있죠. 여기서는 직선 $y=-x$에 대한 대칭이동까지 마저 알아보겠습니다.
직선 $y=x$에 대한 대칭이동 방법을 알아보기 위해 좌표평면 전체를 직선 $y=x$에 대하여 뒤집었고 직각삼각형의 가로, 세로의 길이가 바뀌는 원리를 통해 점 $(a,~b)$가 $(b,~a)$로 이동한다는 사실을 알아보았습니다. 여기서도 원리는 비슷합니다. 다음 그림을 볼까요?
편의상, 제1사분면 위의 점을 하나 잡아서$\textrm{P}(a,~b)$로 놓으면 이 점과 원점을 꼭짓점으로 하고 가로의 길이가$a$, 세로의 길이가$b$인 직각삼각형을 그릴 수 있습니다. 이파란색삼각형을 직선$y=-x$에 대하여 대칭이동한 삼각형이 바로 그림에서초록색 직각삼각형이 되죠. 이때초록색삼각형은 가로의 길이가$b$이고 세로의 길이가$a$가 되어 가로와 세로가 바뀐 것을 확인할 수 있습니다.
단, 이번에는 주목할 점이 하나 더 있어요. 점$\textrm{P}$는 제1사분면 위의 점이었는데 옮겨진 점$\textrm{Q}$는 제3사분면 위에 있죠. 이것은 옮겨진 점의 좌표는 $x,~y$ 좌표가 서로 바뀌는 것뿐만 아니라각 좌표의 부호까지 바뀐다는 것을 알 수 있습니다.
따라서 다음과 같이 정리할 수 있습니다.
예를 들어, 점 $(-1,~4)$를 직선$y=-x$에 대하여 대칭이동한 점의 좌표는$(-4,~1)$이 되며 이 결과는 다음 그림과 같습니다.
● 도형의 대칭이동
지금까지 정리한 대칭이동을 도형의 대칭이동으로 옮겨보겠습니다. 알고 있듯이, 대칭이동은 정방향이든 역방향이든 이동 방법에 차이가 없으므로 도형의 대칭이동은 점의 대칭이동과 다르지 않습니다. 따라서 다음과 같이 정리할 수 있습니다.
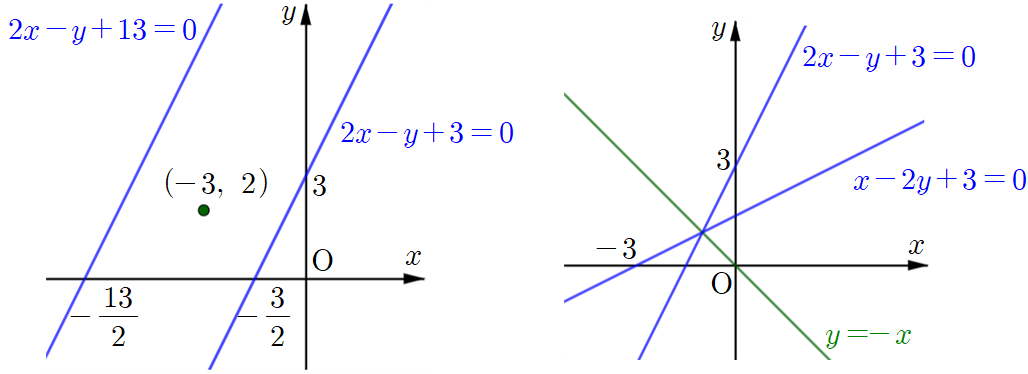
예를 들어, 직선 $2x-y+3=0$을
직선$x=-3$에 대하여 대칭이동하면 $x$ 대신 $-6-x$를 대입하여 $2(-6-x)-y+3=0$, $-2x-y-9=0$, $2x+y+9=0$
직선$y=2$에 대하여 대칭이동하면 $y$ 대신 $4-y$를 대입하여 $2x-(4-y)+3=0$, $2x+y-1=0$
점 $(-3,~2)$에 대하여 대칭이동하면 $x$ 대신 $-6-x$, $y$ 대신 $4-y$를 대입하여 $2(-6-x)-(4-y)+3=0$, $-2x+y-13=0$, $2x-y+13=0$
직선$y=-x$에 대하여 대칭이동하면 $x$ 대신 $-y$, $y$ 대신 $-x$를 대입하여 $-2y+x+3=0$, $x-2y+3=0$
입니다. 각 결과는 다음 그림과 같습니다.
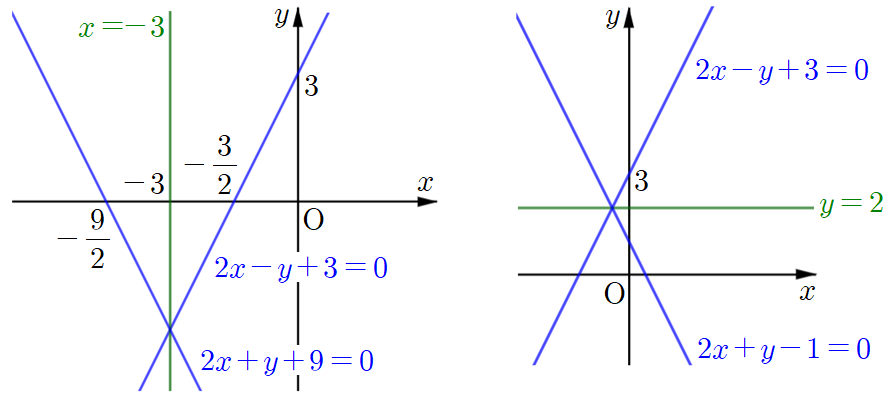
그림은 최고차항의 계수가 $1$이고 $f(-2)=f(4)=0$인 이차함수 $y=f(x)$의 그래프이다.
함수 $y=f(x)$의 그래프와 함수 $y=-f(x)+2$의 그래프의 꼭짓점을 각각 $\textrm{A}$, $\textrm{B}$라 하고, 함수$y=f(x)$의 그래프와 함수 $y=-f(x)+2$의 그래프가 만나는 두 점을 각각$\textrm{C}$, $\textrm{D}$라하자. 사각형 $\textrm{ADBC}$의 넓이는? [2013.11/4점]
① $5\sqrt{10}$ ② $10\sqrt{5}$ ③ $10\sqrt{10}$ ④ $20\sqrt{5}$ ⑤ $20\sqrt{10}$
최고차항의 계수가 $1$이고 $f(-2)=f(4)=0$이므로 인수정리에 의해 이 함수의 식은 $f(x)=(x+2)(x-4)=x^2-2x-8=(x-1)^2-9$임을 알 수 있습니다. 따라서 꼭짓점인 $\textrm{A}$의 좌표는 $(1,~-9)$입니다.
이제$-f(x)+2$를 구해서$f(x)$와 연립하면 되는데 그냥 연립해서 풀 수도 있지만, 여기서는 배운 대칭이동을 써먹어 보겠습니다.
두 식 $-f(x)+2$와 $f(x)$를 더하면 $2$가 되므로 두 식의 평균은 $1$이 되죠. 이 말이 무엇이냐? 두 함수 $y=f(x)$와 $y=-f(x)+2$의 그래프는 다음 그림과 같이$y=1$에 대하여 대칭을 이룬다는 뜻이 됩니다. 따라서 그림에서 빨간색 마름모의 넓이를 구하면 됩니다.
따라서$y=f(x)$와 $y=1$만 연립하면 두 함수의 그래프의 교점을 찾을 수 있죠. 따라서
댓글 영역