고정 헤더 영역
상세 컨텐츠
본문
복잡한 수(큰 수)의 나눗셈의 나머지를 구하는 원리 및 방법 (고1 수학 다항식, 나머지정리의 활용)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
이전 포스팅에서 나머지정리의 원리를 알아봤었습니다. 이 나머지정리를 잘 활용하면 직접 계산으로는 풀 수 없는 복잡한 수를 어떤 수로 나누었을 때의 나머지를 쉽게 구하는 것이 가능해집니다. 여기에서는 그 원리와 요령을 알아보겠습니다.

● 교과서 문제 해설
먼저 서두에 소개된 교과서의 문제를 살펴보겠습니다.

활동1, 2, 3에서 하라는 대로 따라가다 보면 $2018^{10}$을 $2017$로 나눈 나머지를 어렵지 않게 구해낼 수 있습니다. 핵심 원리는 나머지정리를 활용하기 위해 주어진 수에서 특정 부분을 문자로 치환한 다음 다항식의 나눗셈과 항등식의 원리를 이용하는 겁니다.
활동1에서 제시된 다음의 식에 $x=1$을 대입함으로써 $R=1$임을 구할 수 있습니다.
$x^{10}=(x-1)Q(x)+R$
$x^{10}=(x-1)Q(x)+1$
그다음 활동2에서 몫 $Q(x)$를 구하기 위해 식 $x^{10}-1=(x-1)Q(x)$로부터 $x^{10}-1$을 $x-1$로 나누어야 하는데 이때 조립제법을 이용할 수 있습니다. 이때, 나누려는 피제다항식이 무려 10차이므로 다음과 같이 계수 11개를 나열하되 첫 번째 수는 $1$, 마지막 수는 $-1$이고 나머지 계수들은 모두 $0$으로 둔다는 것에 유의합니다.
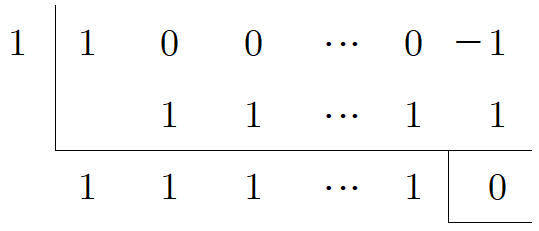
위의 계산에 의해 구하는 $Q(x)$는
$Q(x)=x^9+x^8+ \cdots +x+1$
이제 이 식에서 $x=2018$을 대입하면 $Q(2018)$를 구할 수 있게 되는데 다항식 $Q(x)$는 계수들과 상수항이 모두 $1$이므로 $Q(2018)$이 자연수라는 사실을 확인할 수 있습니다.
이제 활동3에 의해 처음 구한 항등식에서 $x=2018$을 대입하면
$2018^{10}=2017\times Q(2018)+1$
이 되어 $2018^{10}$은 $2017\times Q(2018)+1$로 나타내어짐을 알 수 있죠. 이때, $Q(2018)$은 자연수이므로 $2018^{10}$을 $2017$로 나눈 나머지는 $1$이 됨을 알 수 있습니다.
지금 풀어본 문제는 자연수의 나눗셈이므로 $Q(2018)$이 몫이 됩니다. 따라서 계산 과정에서 $Q(2018)$이 자연수라는 사실을 확인하는 절차가 필요했다는 것을 알 수 있고요. 이 문제에서는 구한 $R=1$이 곧 구하는 나머지가 되었는데 나머지는 0보다 작지 않으면서 2017보다는 작아야 하므로 이 범위에 속하지 않았다면 추가로 나눠주거나 나눈 것을 되가져오는 방식으로 나머지의 범위를 맞추는 과정 또한 필요합니다.
● 제수를 한 문자로 치환한 풀이
위의 풀이에서 $2018$말고 제수인 $2017$을 $x$로 치환하면 $2018=x+1$이 되고 다음과 같이 풀 수 있어요.
$(x+1)^{10}$을 $x$로 나눈 몫과 나머지를 각각 $Q(x)$, $R$이라 하면
$(x+1)^{10}=xQ(x)+R$
위의 식은 항등식이므로 양변에 $x=0$을 대입하면 $R=1$이 되고 $x=2017$을 다시 대입하면 다음 식을 얻을 수 있습니다.
$2018^{10}=2017\times Q(2017)+1$
아까와 비슷한 식이 등장했고 여기서 $2018^{10}$을 $2017$로 나눈 나머지가 $1$임을 입증하려면 $Q(2017)$이 자연수임을 확인해야 합니다. 그런데 위에서 유도한 식 $(x+1)^{10}=xQ(x)+1$의 좌변을 전개하면 계수가 모두 자연수인 다항식이 되고 특히, 최고차항의 계수 및 상수는 $1$임을 알 수 있어요. 그리고 우변에도 상수 $1$이 있으므로
$(x+1)^{10}-1=xQ(x)$
은 양변이 상수항이 없는 다항식이 됩니다. 따라서 식 $Q(x)$는 좌변 $(x+1)^{10}-1$에서 각 항별로 차수만 하나씩 낮춘 식이 되므로 역시 계수가 모두 자연수 다항식이 됩니다. 따라서 $Q(2017)$은 자연수가 됩니다.
이러한 원리를 이해할 수 있으면 조립제법과 같은 나눗셈을 일일이 하지 않고도 원하는 나머지를 쉽게 구할 수 있어요. 따라서 이러한 문제가 등장하면 피제수에서 치환할 문자를 찾는 것보다는 제수 자체를 한 문자로 치환하는 풀이가 좀 더 유리합니다.
● 나머지 구하는 원리의 일반화
이제 위의 풀이를 일반화하기 위해 정수 $m$과 자연수 $k$를 가정하고 계수가 정수인 다항식 $f(t)$에 대하여 $f(m)$을 $k$로 나눈 나머지를 구하는 상황을 생각해 보겠습니다. 예를 들어 위의 교과서 문제의 경우는 $m=2018$, $k=2017$이고 $f(t)=t^{10}$으로 생각하여 $f(m)=2018^{10}$을 $k=2017$로 나눈 나머지를 구하는 문제로 볼 수 있었죠.
바로 위에서 푼 것과 같이 제수인 $k$를 문자 $x$로 놓고 시작합니다. 그리고 $m$을 $k=x$가 포함된 식으로 나타내기 위해 다음과 같이 가정합니다. 여기서 $a$, $b$는 정수입니다.
${\color{Red}m}=a{\color{Blue}k}+b=a{\color{Blue}x}+b$
이제 $f(m)$을 $k$로 나눈 나머지를 구하기 위해 $f(ax+b)$를 $x$로 나눈 나머지를 구하는 상황을 생각합니다.
여기서 $f(ax+b)$는 다항식이죠. 다항식 $f(ax+b)$를 $x$로 나눈 몫과 나머지를 각각 $Q(x)$, $R$이라 하면 다음의 식을 유도할 수 있어요. 또한, 이 식은 $x$에 대한 항등식이므로 $x=0$을 양변에 대입하여 $R$의 값도 바로 구할 수 있습니다.
${\color{Red}f(ax+b)}=xQ(x)+R$, ${\color{Red}f(b)}=R$
이 식에다 다시 $x=k$와 ${\color{Red}m}=a{\color{Blue}k}+b$를 대입하면
$f(m)={\color{Red}f(ak+b)}=kQ(k)+{\color{Red}f(b)}$
여기서 $f(b)=R$의 값이 구하는 나머지임을 확신할 수는 없지만, 적어도 $f(m)$을 $k$로 나눈 나머지는 $f(b)=R$을 $k$로 나눈 나머지와 일치한다는 사실은 확인할 수 있어요.
따라서 이 결과는 다음과 같이 정리할 수 있습니다.
| 복잡한 정수를 자연수로 나눈 나머지 |
| 자연수 $k$, 정수 $a$, $b$, 계수가 정수인 다항식 $f(x)$에 대하여 정수 $f(ak+b)$를 $k$로 나눈 나머지는 $f(b)$를 $k$로 나눈 나머지와 일치한다. |
여기서 다항식 $f(x)$는 우리가 원하는 어떠한 형태든 가능합니다. 따라서 이 원리를 이용하면 $f(ak+b)$를 $k$로 나눈 나머지를 구하기 위해 $f(ak+b)$를 $f(b)$로 바꿔서 문제를 풀 수 있게 되죠. 이때 $b$의 값이 최대한 작도록 수를 변형해 주는 것이 계산 부담을 덜어주는 포인트입니다. 그리고 이 과정은 계속해서 반복할 수 있기 때문에 결국 아무리 복잡한 수를 제시해도 나머지정리를 잘 이용하면 어떤 자연수로 나눈 나머지는 어렵지 않게 구할 수 있음을 의미하게 됩니다.
● 정수의 나눗셈
학교에서는 나눗셈의 몫과 나머지를 배울 때 자연수를 자연수로 나누는 경우만 다루었는데 위의 원리를 자유롭게 이용할 수 있으려면 피제수의 대상을 자연수에서 정수로 확장할 필요가 있습니다.
예를 들어 12를 5로 나눈다고 할 때 몫은 2, 나머지도 2가 나옵니다. 이때, 5로 나누었을 때 나머지가 똑같이 2가 되는 수는 7도 있고 2도 있죠. 이들을 몫과 나머지로 표현하면 다음과 같습니다. 식에서 하늘색으로 표시한 값이 몫이 되죠.
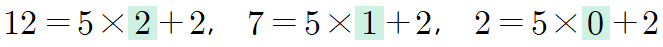
여기에서 끝나는 게 아니라 몫이 음수가 나오는 경우도 생각하면 피제수의 범위를 다음과 같이 음의 정수까지 확장할 수 있습니다.
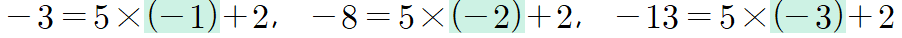
피제수를 정수로 확장해도 제수는 자연수이고 $0\leq $(나머지)$<$(제수) 인 관계는 유지됩니다.
예를 들어 $-52$를 $7$로 나눈 몫과 나머지를 구해볼게요. 이때, $52=7\times 7+3$임을 이용하면
$-52=7\times (-7)-3$
인데 여기서 나머지를 $-3$이라 하면 안 되고 다음의 계산과정을 더 거칩니다.
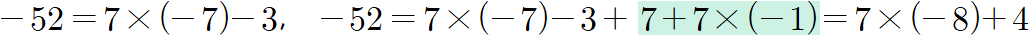
따라서 몫은 $-7$이 아닌 $-8$이 되며 나머지는 $4$입니다.
● 연습문제 풀이

$70^{10}+21^9$을 $23$으로 나눈 나머지를 구하시오.
위에서 정리한 이론에 의하면 복잡한 피제수가 등장해도 제수를 반복적으로 빼면서 피제수의 크기를 줄이는 요령을 이용할 수 있어요.
위에서 70의 경우는 $70~→~23\times 3+1~→~1$
21의 경우는 $21~→~-2$
이므로 문제에 제시된 제수 $70^{10}+21^9$은 $1^{10}+(-2)^9=-511$로 바꿀 수 있습니다. 즉, $-511$을 $23$으로 나눈 나머지를 구하면 되는 거죠. 이제
$-511=23\times (-23)+18$
이므로 구하는 나머지는 $18$입니다.
피제수 $70^{10}+21^9$을 $1^{10}+(-2)^9=-511$로 바꾼 원리를 나머지정리를 이용하여 자세히 설명하면 다음과 같습니다.
| $23=x$라 하면 $70^{10}+21^9=(3x+1)^{10}+(x-2)^9$ 따라서 다항식 $(3x+1)^{10}+(x-2)^9$을 $x$로 나눈 몫과 나머지를 각각 $Q(x)$, $R$이라 하면 $(3x+1)^{10}+(x-2)^9=xQ(x)+R$ 이 식은 항등식이므로 양변에 $x=0$을 대입하면 $1^{10}+(-2)^9=R$, $R=-511$ 이제 양변에 $x=23$을 대입하면 $70^{10}+21^9=23\times Q(23)-511$ 즉, $70^{10}+21^9$을 $23$으로 나눈 나머지는 $-511$을 $23$으로 나눈 나머지와 같다. |

$301\times 302\times 303\times 304$를 $5$로 나눈 나머지를 구하시오.
각각의 수를 $5$로 나눈 나머지로 만든 다음의 수를 이용하여 나머지를 구할 수 있습니다.
$1\times 2\times 3\times 4=24$
이제 $24$를 $5$로 나눈 나머지는 $4$이므로 답은 $~4~$입니다.

$2^{100}$을 $23$으로 나눈 나머지를 구하시오.
거듭제곱을 어느 정도 해준 다음 $23$씩 빼는 방법으로 접근합니다. 이때 $2^6=64$이고 $23\times 3=69$이므로
$2^{100}=(2^6)^{16}\times 2^4=64^{16}\times 2^4$
$64^{16}\times 2^4~{\color{Red}→}~(-5)^{16}\times 2^4$
$(-5)^{16}\times 2^4=25^8\times 2^4$
$25^8\times 2^4~{\color{Red}→}~2^8\times 2^4$
$2^8\times 2^4=2^6\times 2^6=64\times 64$
$64\times 64~{\color{Red}→}~(-5)\times (-5)=25$
$25~{\color{Red}→}~2$
따라서 구하는 나머지는 $~2~$입니다.
♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 다항식' 카테고리의 다른 글
| 치환을 이용한 인수분해, 상반다항식의 인수분해 (고1 수학 다항식) (0) | 2023.06.08 |
|---|---|
| 다항식의 인수분해의 개념 및 기초 (고1 수학 다항식) (4) | 2023.05.31 |
| 조립제법의 원리 및 활용에 대한 자세한 이해 (고1수학 다항식의 나눗셈) (2) | 2023.04.22 |
| 나머지정리에 대한 자세한 이해 (고1수학 다항식) (2) | 2023.04.20 |
| 항등식에 대한 자세한 이해 (고1수학 다항식) (0) | 2023.04.19 |





댓글 영역