나머지정리에 대한 자세한 이해 (고1수학 다항식)

나머지정리에 대한 자세한 이해 (고1수학 다항식)

 

 안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.

 직전 포스팅에서 항등식에 대한 개념을 다루었는데 그 이유는 오늘 다룰 내용인 나머지정리를 유도하는 데 핵심 원리가 되기 때문입니다. 여기서 나머지는 다항식의 나눗셈에서 발생하는 그 나머지를 말하는데 우리가 나눗셈을 할 때는 대체로 일차식으로 나누는 경우가 많습니다. 그리고 일차식으로 나눌 때는 특성상 나머지는 항상 상수가 되는데, 이렇게 다항식을 일차식으로 나눌 때 나타나는 성질을 좀 더 알아보는 단원이 나머지정리입니다. 그리고 이 원리를 통해 인수분해를 하기 위한 중요한 기술을 얻을 수 있습니다.

● 나머지정리

나머지정리에 대한 내용을 간단히 요약하면 다음과 같습니다. 위에서도 말했듯이 이것을 유도하는 핵심 원리는 몫과 나머지의 개념과 항등식입니다.

 간단한 원리죠? 나눗셈 결과를 몫과 나머지로 나타내고 수치대입법을 한 번 적용했더니 $R=f(\alpha )$라는 결과가 나왔습니다. 앞에서 다항식의 나눗셈을 할 때, 세로셈으로 직접 나눠서 몫과 나머지를 구하는 연습을 많이 했는데, 일차식으로 나눌 경우에는 직접 계산하지 않고 다항식에 수치 하나만 대입함으로써 나머지를 간단하게 구할 수 있는 개념이 바로 나머지정리입니다. 이 내용을 일차식의 일반적인 형태인 $ax+b$로 바꿔서 다시 정리하면 다음과 같습니다.

즉, 나머지정리의 핵심은 일차식으로 나눌 때의 나머지를 구하고 싶으면 일일이 나눗셈 계산을 하지 않고도 그 일차식의 값이 0이 되는 $x$의 값을 피제다항식에 대입해서 구할 수 있다는 겁니다.

 

● 나머지정리와 직접 나눗셈과의 비교

예를 들면 예전 포스팅에서 $3x^2+4x+5$를 $x+2$로 나누는 걸 다음과 같이 계산했습니다.

이제 $x=-2$를 $3x^2+4x+5$에다 대입하면

$3\times (-2{)}^2+4\times (-2)+5=9$

가 되어 위에서 구했던 나머지와 일치하는 것을 알 수 있습니다.

 또한, 예전에 풀어본 예제 중에 다항식 $A$를 구하기 위해 다음과 같이 $2x^3+3x^2-x-1$을 $2x+1$로 나누었습니다.

이 문제도 마찬가지로 일차식 $2x+1$의 값이 0이 되는 $x=-\frac{1}{2}$을 대입해 보면

이 되어 역시 나눗셈에서 구한 나머지인 0과 일치하는 걸 알 수 있습니다.

 결국 아무리 복잡한 다항식이라도 일차식으로 나눈 나머지는 수치만 대입해서 계산할 수 있다는 거죠. 예를 들어, 다항식 $f(x)=x^{100}+x^{50}+2$을 $x+1$로 나눈 나머지를 직접 계산을 통해 구하려면 엄청난 계산을 해야 하지만 나머지정리를 이용하면 $f(-1)=(-1{)}^{100}+(-1{)}^{50}+2=4$와 같이 매우 간단히 구할 수 있게 됩니다.

 물론 나머지정리는 몫까지 구하지는 못합니다. 그러나 나머지정리만으로 우리는 임의의 다항식이 일차식으로 나누어 떨어지는지 아닌지를 판단할 수 있으며, 이는 곧 인수분해의 핵심원리인 인수정리로 이어집니다. 또한 나머지정리로부터 복잡한 다항식을 다루는 유형들을 많이 물어볼 수 있으므로 이제부터 소개하는 예제들을 잘 숙지하고 가셔야 합니다.

반응형

● 나머지정리 관련 연습문제 풀이

 

다항식 $P(x)$를 $x+2$로 나누었을 때의 나머지는 $-3$이고, $x-3$으로 나누었을 때의 나머지는 2이다. $P(x)$를 $x^2-x-6$으로 나누었을 때의 나머지를 구하시오.

나머지정리의 교과서 대표유형입니다. 다항식 $P(x)$의 정보가 안 나와 있으므로 직접적인 나눗셈을 할 수 없는 상태입니다. 따라서 이런 유형에서 사용되는 원리가 나머지정리입니다.

나머지정리에 따라 문제의 조건들을 식으로 변환하면

$P(-2)=-3$,  $P(3)=2$

이제 $P(x)$를 $x^2-x-6$으로 나누었을 때의 나머지를 $ax+b$라 합니다. 나머지 식을 왜 이렇게 세워야 할까요? 제다항식인 $x^2-x-6$이 이차식이므로 나머지의 차수는 그보다 작은 일차식이나 상수가 되어야 하기 때문입니다. 실제로 구한 나머지가 상수인지 일차식인지는 $a$가 $0$인지 $0$이 아닌 수인지에 따라 결정되겠죠. 그리고 이때의 몫을 $Q(x)$로 놓으면 다음과 같이 식을 만들 수 있습니다.

$P(x)=(x^2-x-6)Q(x)+ax+b$

그리고 $x^2-x-6$은 $(x+2)(x-3)$으로 인수분해 되므로

$P(x)=(x+2)(x-3)Q(x)+ax+b$

이제부터 어떻게 해야 할지 감이 오시나요? 나머지정리로부터 얻은 조건 $P(-2)=-3$, $P(3)=2$를 각각 대입하면 $Q(x)$가 사라지면서 $a$, $b$에 대한 연립방정식을 만들 수 있습니다.

$P(-2)=-2a+b=-3$,  $P(3)=3a+b=2$

연립방정식을 풀면 $a=1$, $b=-1$이므로 구하는 나머지는 $x-1$입니다.

---

 

다항식 $f(x)$를 $(x+1{)}^2$으로 나누었을 때의 나머지는 $-2x+3$이고, $x-2$로 나누었을 때의 나머지는 17이다. $f(x)$를 $(x+1{)}^2(x-2)$로 나누었을 때의 나머지를 $R(x)$라 할 때, $R(0)$의 값을 구하시오.

예제1에서 한 단계 발전된 유형입니다. $f(x)$를 삼차다항식으로 나누기 때문에 나머지는 상수부터 이차식까지 될 수 있습니다. 따라서 문제에서 구하려는 나머지 $R(x)$를 $a{x}^2+bx+c$라고 놓겠습니다. 그리고 몫을 $Q(x)$로 놓으면 다음식을 만들 수 있습니다.

$f(x)=(x+1{)}^2(x-2)Q(x)+a{x}^2+bx+c$

그다음 $f(x)$를 $(x+1{)}^2$으로 나누었을 때의 나머지가 $-2x+3$이라고 했는데 이걸 어떻게 적용하는지 잘 보셔야 합니다.

위의 등식을 보면 $(x+1{)}^2(x-2)Q(x)$는 이미 $(x+1{)}^2$의 배수이죠? 그럼 이 식까지는 이미 $(x+1{)}^2$로 나눗셈이 끝났다는 얘기입니다. 그럼 남아 있는 식인 $a{x}^2+bx+c$만 $(x+1{)}^2$로 나누면 그 나머지가 바로 $-2x+3$가 되어야 하는 거죠. 이제 직접 나눗셈을 하면 몫은 상수 가 되므로

$R(x)=a{x}^2+bx+c=$ $a$ $(x+1{)}^2$ $-2x+3$

가 됩니다. 이렇게 하면 3개였던 미지수가 하나로 줄어들었죠? 이제 남은 조건인 $f(x)$를 $x-2$로 나누었을 때의 나머지가 17인 것만 적용하면 $a$까지 구할 수 있습니다. 나머지정리에 의해 $f(2)=17$이므로

$f(2)=R(2)=a\times 3^2-2\times 2+3=9a-1=17$
$a=2$

따라서 $R(x)=2(x+1{)}^2-2x+3$이므로 $R(0)=$5 입니다.

---

 

삼차다항식 $f(x)$가 다음 조건을 만족시킨다.

(가) $f(1)=2$ (나) $f(x)$를 $(x-1{)}^2$으로 나눈 몫과 나머지가 같다.

$f(x)$를 $(x-1{)}^3$으로 나눈 나머지를 $R(x)$라 하자. $R(0)=R(3)$일 때, $R(5)$의 값을 구하시오.  [2015.06.교육청/4점]

㈏ 조건을 통해 다항식 $f(x)$의 틀을 잡아보겠습니다. $f(x)$가 삼차식이므로 $(x-1{)}^2$으로 나눈 몫은 일차식이 되어야겠죠? 이 식을 $ax+b$라고 하면 몫과 나머지가 같다고 했으니까

$f(x)=(x-1{)}^2(ax+b)+ax+b$

와 같이 식을 세울 수 있습니다. 여기에다 $f(1)=2$까지 적용하면 미지수를 줄일 수 있겠죠.

$f(1)=a+b=2$,  $b=-a+2$
$f(x)=(x-1{)}^2(ax-a+2)+ax-a+2$

문제에서는 $f(x)$를 $(x-1{)}^3$으로 나눈 나머지에 관심을 보입니다. 따라서 구한 $f(x)$에 $(x-1{)}^3$이 포함되도록 식을 조작해 주는 것이 이 문제의 핵심아이디어인데 여기서는 $ax-a+2$를 $x-1$로 나눈 몫과 나머지를 이용하여 $ax-a+2=a(x-1)+2$임을 이용합니다.

$f(x)=(x-1{)}^2\{a(x-1)+2\}+a(x-1)+2$
$=$ $a(x-1{)}^3$ $+$ $2(x-1{)}^2+a(x-1)+2$

따라서 $R(x)=2(x-1{)}^2+a(x-1)+2$입니다. 이제 마지막 조건 $R(0)=R(3)$을 이용하면

$2-a+2=8+2a+2$,  $-3a=6$,  $a=-2$

따라서

$R(x)=2(x-1{)}^2-2(x-1)+2$

이므로 $R(5)=$26입니다.

---

 

● 인수정리

앞에서 언급한 대로 나머지정리는 임의의 다항식을 일차식으로 나눌 때, 나누어 떨어지는지 아닌지를 판단할 수 있으며 이것은 아래의 인수정리로 이어집니다.

$P(x)$를 일차식 $x-\alpha$로 나눈 나머지가 $P(\alpha )$이므로 나머지정리에 의해 위의 인수정리는 자명합니다. 마찬가지로 인수정리도 일반적인 일차식 $ax+b$로 설명하면 다음과 같습니다.

 위에서 $2x^3+3x^2-x-1$을 $2x+1$로 나눈 나머지가 다음의 계산에 의해 0임을 확인했었죠. 이 경우 인수정리에 의해 $2x^3+3x^2-x-1$은 $2x+1$로 나누어 떨어진다고 할 수 있습니다.

 

$x$에 대한 다항식 $2x^3+a{x}^2+bx+6$이 $x^2-1$로 나누어 떨어질 때, $ab$의 값은? (단, $a$, $b$는 상수이다.)  [2014.06.교육청/3점]

① $6$     ② $8$     ③ $10$     ④ $12$     ⑤ $14$

$x^2-1=(x-1)(x+1)$이므로 주어진 다항식은 $x-1$로도 나누어 떨어지고 $x+1$로도 나누어 떨어집니다. 여기서 이용되는 개념이 바로 인수정리죠.

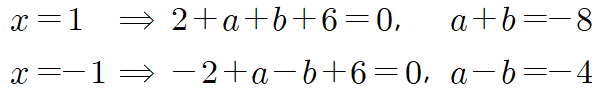
연립방정식을 풀면 $a=-6$, $b=-2$입니다. 따라서 $ab=12$이므로 답은 ④번입니다.

---

 

♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.