원의 (표준형)방정식에 대한 자세한 이해 (고1수학 도형의 방정식)

원의 (표준형)방정식에 대한 자세한 이해 (고1수학 도형의 방정식)

자연 현상 속의 원 (그림 출처: pixabay)

 안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽게 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.

 오늘부터는 도형의 방정식 단원에서 원에 방정식에 대한 개념을 다뤄보겠습니다. 직선의 방정식은 $x$, $y$에 대한 일차식이므로 이전부터 자주 다뤘던 친숙한 개념이었죠. 그러나 원의 방정식부터는 전혀 새로운 방정식의 형태를 공부하게 됩니다. 원은 넓이 개념이 존재하는 평면도형 중에서는 가장 간단하게 정의하고 방정식으로 표현할 수 있는 도형이라 할 수 있습니다. 그러면서도 원 안에는 $\pi$와 같은 심오한 개념과 함께 삼각비와 같은 다양한 성질이 들어있으며, 실생활에서도 그 활용의 예를 무수히 찾을 수 있죠. 수학에서도 원은 매우 중요한 도형입니다. 이러한 원은 방정식으로 어떻게 나타내는지 알아보도록 하겠습니다.

● 원의 정의

원의 방정식을 유도하기 위해 가장 먼저 확인할 일은 원의 정의입니다. 원이란 평면 위의 한 정점에서 일정한 거리에 있는 모든 점으로 이루어진 도형입니다. 원은 평면도형이므로 평면이라는 전제가 붙는다는 것을 유의해야겠죠. 평면이란 조건 없이 공간에서 같은 문장으로 정의하면 구가됩니다.

우리는 초등학교나 중학교에서 위의 그림처럼 컴퍼스에 연필을 끼우고 종이에다가 컴퍼스의 뾰족한 부분을 대고 원을 그려 본 경험이 있을 것입니다. 이때 종이에 댄 뾰족한 부분이 원의 중심이 되고 뾰족한 부분과 연필과의 거리가 반지름이 됩니다. 즉, 하나의 원을 결정하기 위해 중심과 반지름의 길이가 필요한 거죠.

평면 좌표에서도 하나의 원의 방정식을 만드는데 필요한 조건은 중심과 반지름의 길이입니다. 이제 점 $\textrm{C}(a,~b)$를 중심으로 하고 반지름의 길이가 $r$인 원의 방정식을 구해보도록 하겠습니다.

 

● 원의 (표준형) 방정식

원의 방정식을 만드는 원리는 간단합니다. 도형 위의 임의의 한 점을 $\textrm{P}(x,~y)$로 놓고 이 점의 좌표 $x$, $y$가 만족하는 관계식을 유도하면 됩니다. 이때, 점 $\textrm{P}$가 원의 어느 위치에 있든 위에서 정의했던 대로 딱 한 가지 성질을 만족하게 되죠. 바로 원의 중심 $\textrm{C}(a,~b)$와의 거리가 $r$이라는 점입니다. 따라서 다음의 관계식으로부터 원의 방정식이 바로 완성됩니다.

반대로 이 방정식을 만족하는 점 $\textrm{P}(x,~y)$는 점 $\textrm{C}(a,~b)$와의 거리가 $r$로 일정하므로 중심이 점 $\textrm{C}(a,~b)$이고 반지름의 길이가 $r$인 원을 그립니다.

 이상으로부터 다음과 같이 정리할 수 있습니다.

 

● 관련 연습문제

 

● 좌표축에 접하는 원의 방정식

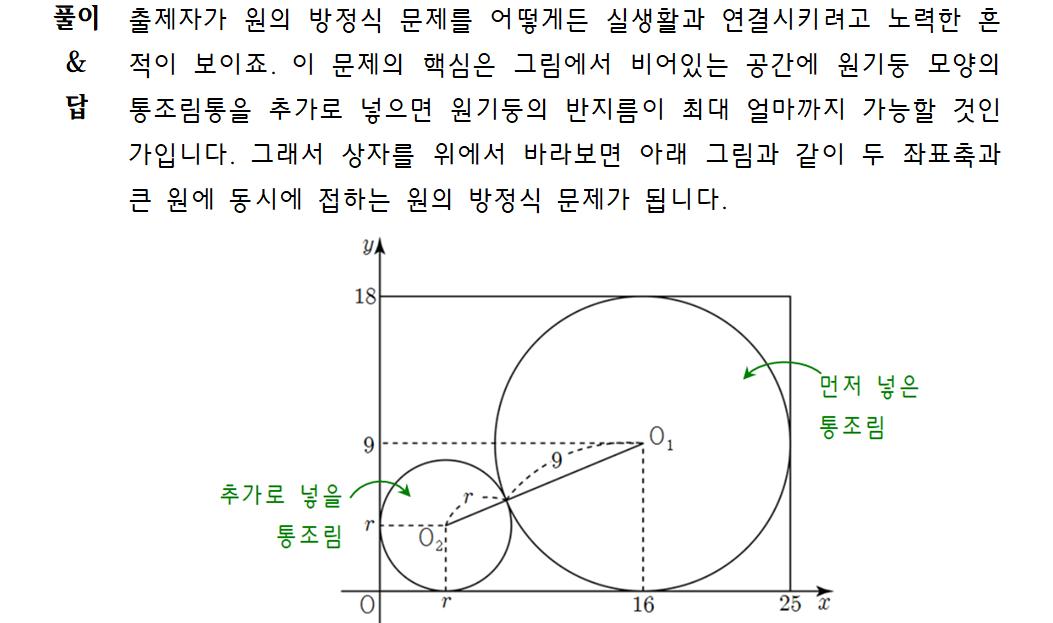
원이 좌표축에 접하면 원의 중심에서 접하는 축까지의 거리가 곧 원의 반지름이 됩니다. 이 경우 원의 중심의 좌표는 접하는 축에 따라 다음과 같이 분류됩니다. 당연히 이건 외워야 하는 공식은 아니고 방정식을 보면서 왜 이런 식이 되어야 하는지 스스로 생각해보시기 바랍니다.

 

♥ 이해가 잘 되셨다면 좋아요와 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.