고정 헤더 영역
상세 컨텐츠
본문

원과 직선의 위치 관계에 대한 자세한 이해 (고1수학 도형의 방정식)


안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.

오늘부터는 원에 직선을 첨가한 내용인 원과 직선의 위치 관계에 대해 알아봅니다. 이미 교과서의 앞 단원에서 이차함수의 그래프와 직선의 위치 관계를 다룬 적이 있습니다. 마찬가지로 원도 직선과의 위치 관계는 매우 중요하게 다루어집니다. 대부분의 원의 방정식 기출문제도 원 하나만 가지고 내는 것보단 직선을 같이 끼어서 내는 문제가 훨씬 많죠. 따라서 여기부터는 좀 더 마음을 다 잡고 공부하시기 바랍니다.
● 직선과 원의 중심 사이의 거리를 이용한 위치 관계
일반적으로 원과 직선의 위치 관계는 다음 3가지로 나뉩니다. 이차함수 때와 마찬가지로 위치 관계를 나누는 기준은 원과 직선이 만나서 생기는 교점의 개수로 결정하며 교점은 최소 0개부터 최대 2개까지 존재합니다. 그리고 이 관계는 직선과 원의 중심까지의 거리

특히, 위에서


● 판별식을 이용한 위치 관계
이차함수와 직선의 위치 관계에서는 이차방정식의 판별식을 이용하여 이들의 위치 관계를 나눈 바 있습니다. 마찬가지로 원은
예를 들어 원

와 같이 이차방정식이 만들어집니다. 그렇다면 이 방정식의 실근이 바로 원과 직선의 교점의

● 위치 관계 연습 문제 풀이

원과 직선이 서로 다른 두 점에서 만날 경우, 가장 흔히 물어볼 수 있는 문제는 두 교점 사이의 거리를 구하는 것입니다. 아래의 문제는 독특한 3점짜리 기출문제라 풀이1과 풀이2의 계산이 다소 복잡하게 나타나지만, 이 방법이 보편적으로 쓰이므로 그 원리를 잘 이해하고 가시기 바랍니다.
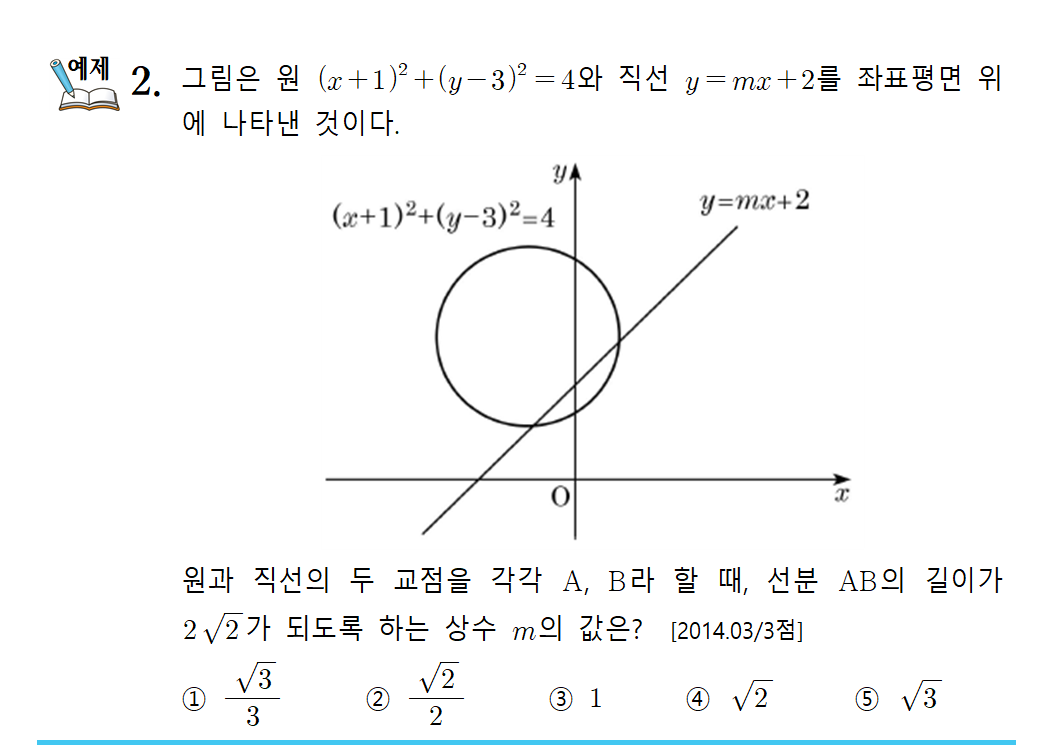




3점짜리 기출문제인데 직선의 기울기에 미지수
문제를 지혜롭게 풀어내려면 출제자의 의도를 눈치껏 파악하는 것도 필요합니다.




함수

위의 gif의 움직임을 관찰해보면 그래프가 제2사분면에서 만날 때는 이미 제1사분면에서 서로 다른 두 점에서 만나는 상태이므로 교점이 3개부터 4개까지 나옴을 알 수 있죠. 따라서 서로 다른 두 점에서만 만나도록 하려면 제2사분면에서는 만나지 않아야 하고 제1사분면에서만 교점이 두 개가 생기도록 해야 합니다. 이해를 돕기 위해 그래프 프로그램을 이용했지만, 위와 같은 움직임은 여러분이 스스로 생각할 수 있어야 합니다.


♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 도형의 방정식' 카테고리의 다른 글
| 접점이 주어진 원의 접선의 방정식에 대한 자세한 이해 (고1수학 도형의 방정식) (0) | 2022.06.29 |
|---|---|
| 기울기가 주어진 원의 접선의 방정식에 대한 자세한 이해 (고1수학 도형의 방정식) (0) | 2022.06.28 |
| 아폴로니오스의 원에 대한 확실하고도 쉬운 이해 (고1수학 도형의 방정식) (0) | 2022.06.26 |
| 원의 방정식의 일반형에 대한 자세한 이해 (고1수학 도형의 방정식) (6) | 2022.06.23 |
| 원의 (표준형)방정식에 대한 자세한 이해 (고1수학 도형의 방정식) (0) | 2022.06.22 |





댓글 영역