고정 헤더 영역
상세 컨텐츠
본문
논란의 요일 계산 문제 "어제가 내일이었으면 좋겠다."의 자세하고 확실한 해설


안녕하세요? 수학 이슈에 대해 남다르게 해석하는 Holymath입니다. 오늘 다룰 주제는 엄청나게 화제가 되었던 요일 계산 문제입니다. 사실 오늘 다룰 문제는 수학 문제라기보다는 국어 문제에 가까운데요. 어떤 문제가 그렇게 화제가 되었는지 보도록 하겠습니다.

● 문제 소개
화제가 된 문제는 다음과 같습니다.

매우 간단한 문장으로 되어있지만, 이 문제를 처음 보신 분이라면 누구라도 꽤나 오랜 시간을 고민할 겁니다. 그리고 대부분은 답을 ④번으로 택합니다.
그런데 이 문제는 2014년도에 이슈가 되어 이미 국립국어원에서도 ①, ④번으로 복수 정답으로 결론을 내렸던 문제입니다. 그러나 이 문제에 대해 여전히 어리둥절하신 분들이 많아 각종 블로그나 유튜브에서도 계속 다루어지고 있습니다. 문제적 남자(https://youtu.be/oqhIlwDAxg4)에도 이 문제가 나온 적이 있었고, 최근에는 구독자 80만 명인 빠더너스의 문쌤도 이 문제를 풀어줬죠.

결론을 내려줬다고 하는 국립국어원에는 같은 주제로만 수도 없이 많은 질문이 올라와 있습니다. 여기서 페이지를 넘겨도 같은 주제로 된 질문들이 수두룩합니다.
위의 질문은 여러 사람이 하긴 했지만 그중에서도 답변을 인정하지 못하고 유독 많은 질문을 하는 사람도 한 명 있습니다. 이 정도면 그냥 "빨리 내 생각이 맞다고 해줘라"인지...

최초의 질문은 다음과 같이 2014년 12월 12일에 올라왔고 지금은 오래돼서 그런지 검색해도 잘 안 나오더군요.
이런 질문이 지금까지도 올라오고 있으니 국립국어원 관계자도 참 고생이 많을듯합니다. 관련된 포스팅을 검색해 보면 지금까지도 일요일이 답인 것은 인정하지만 수요일은 인정할 수 없다는 글도 있죠.
● 문제 해설
그렇다면 답이 왜 복수가 되는지 문제 해설에 들어가 보겠습니다.
| [문제] 어제가 내일이었으면 좋겠다. 그럼 오늘이 금요일일텐데... 그렇다면 오늘은 무슨 요일일까? ① 수요일 ② 목요일 ③ 금요일 ④ 일요일 |
문제의 논란은 첫 문장에서 시작됩니다. "어제가 내일이었으면 좋겠다." 앞 뒤 문맥을 봤을 때, '어제'와 '내일'은 이 두 개념을 똑같이 두겠다는 뜻이 아니라 한쪽 시간을 다른 쪽 시간으로 옮기고 싶다는 뜻을 나타냅니다.
즉, 수학적으로 접근하면 어제와 내일을 대응시키는 개념이죠. 대응은 두 집합 간의 원소끼리 짝 지어주는 개념으로 함수 단원에서 등장하는 단어입니다.
그런데 대응에는 두 가지 방법이 있습니다. 바로 다음과 같이 어제를 내일로 대응시키는 것과 내일을 어제로 대응시키는 것이죠.
1. 어제 → 내일 2. 내일 → 어제
1번처럼 어제를 내일로 대응시키는 것은 다음과 같이 어제를 내일로 이동시킨다는 겁니다. 만약 어제, 오늘, 내일이 13, 14, 15일이라면 어제의 13일을 내일로 옮겨서 내일의 날짜를 13일로 만들고 싶다는 뜻이 되는 거죠.
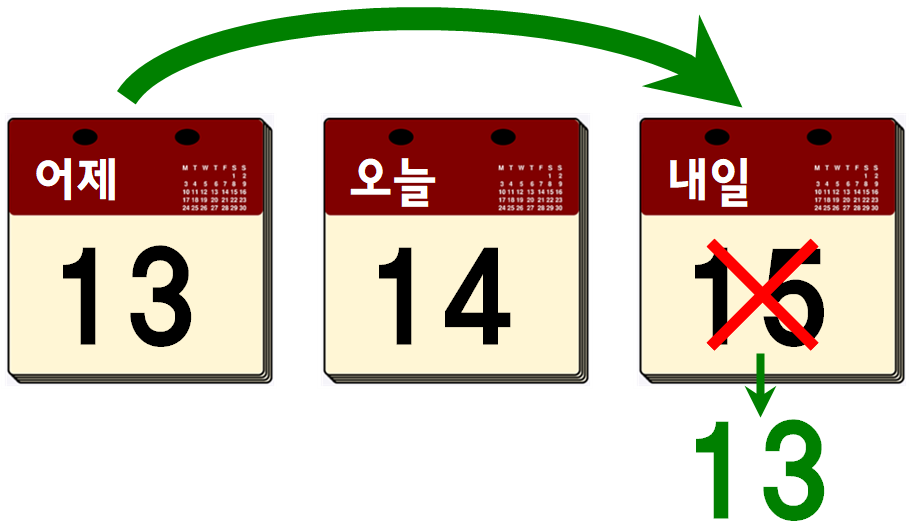
이렇게 내일을 13일로 만들면 어제와 오늘의 날짜는 각각 11일, 12일이 되겠죠. 즉, 어제를 내일로 옮기는 것은 시간상으로 2일 전으로 돌아가고 싶다는 뜻이 됩니다. 2일 전으로 돌아갔는데 금요일이 된다면 실제 오늘의 날짜는 일요일이 됩니다.
반면, 2번처럼 내일을 어제로 대응시키는 것은 다음과 같이 내일을 어제로 이동시킨다는 겁니다. 만약 어제, 오늘, 내일이 13, 14, 15일이라면 내일의 15일을 어제로 옮겨서 어제의 날짜를 15일로 만들고 싶다는 뜻이 되는 거죠.
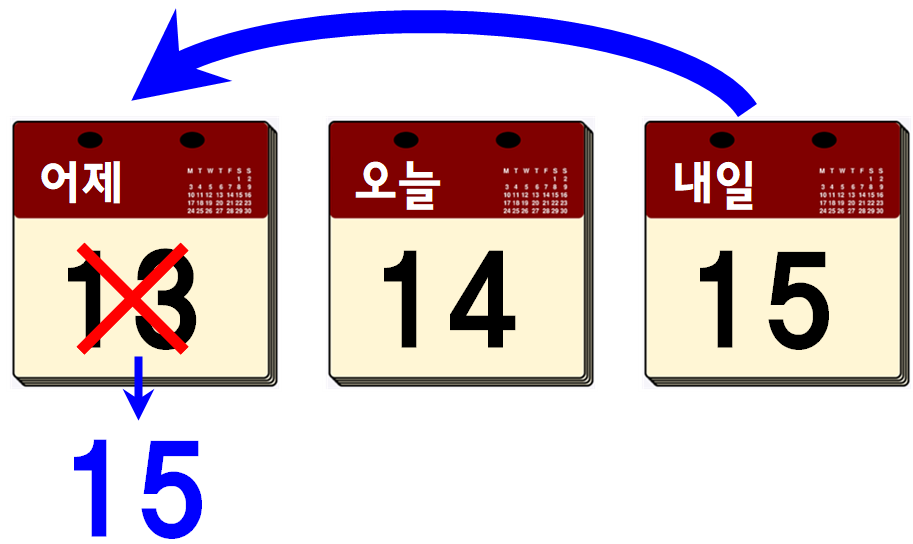
이렇게 어제를 15일로 만들면 오늘과 내일의 날짜는 각각 16일, 17일이 되겠죠. 즉, 내일을 어제로 옮기는 것은 시간상으로 2일 후로 건너뛰고 싶다는 뜻이 됩니다. 2일 후로 갔는데 금요일이 된다면 실제 오늘의 날짜는 수요일이 됩니다.
이상을 정리하면 다음과 같습니다.
| 어제가 내일이었으면 좋겠다. 1. 어제를 내일로 옮기고 싶다 → 2일 전으로 돌아가고 싶다 → 2일전 오늘이 금요일이라면 오늘은 일요일이다 2. 내일을 어제로 옮기고 싶다 → 2일 이후로 가고 싶다 → 2일 후 오늘이 금요일이라면 오늘은 수요일이다 |
따라서 정답은 ①, ④번으로 복수 정답이 됩니다. 추가적으로 위의 논리는 빠더너스 문쌤 영상의 베댓과도 일치합니다.
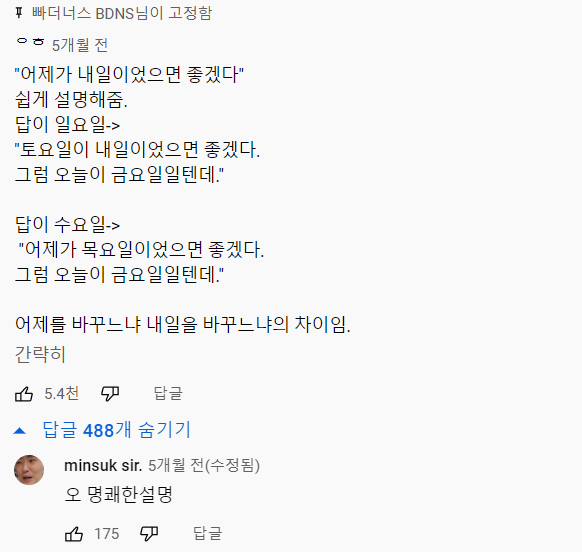
● 반박 주장들
그런데 국립국어원에 무수히 많은 질문이 있듯이 위의 베댓에서도 수백 개의 대댓글이 달려있네요. 읽어보면 죄다 수요일이 답인 것을 인정하지 못해서 논쟁하는 내용입니다. 이들은 왜 이렇게 수요일을 답으로 인정하지 못하는 걸까요?
가장 많은 이유는 주어가 '어제'라는 점에 있습니다. "어제가 내일이었으면 좋겠다"고 했으므로 어제를 움직여서 내일로 옮기는 뜻이 될 수는 있어도 내일을 움직이는 뜻이 될 수는 없다는 의견이죠. 만약 수요일이 답이 되려면 "어제가 내일이었으면 좋겠다"가 아니라 "내일이 어제였으면 좋겠다"가 되어야 한다고 주장합니다.
그런데 과연 그럴까요? 문제에 쓰인 문장에서 핵심은 "어제가 내일이다"입니다. 주인공이 바라는 점이죠. 그런데 이 문장만 놓고 보면 "어제가 내일이다."와 "내일이 어제이다"는 다를 것이 1도 없습니다.
"A는 B이다." $\Leftrightarrow $ "B는 A이다."
→ "A=B이다." $\Leftrightarrow $ "B=A이다."
이것은 수학에서 기본 중에 기본으로 쓰이는 논리이죠. 수학이 아니라 국어 문법상으로도 이 두 문장이 다르게 해석될 수는 없습니다. 이러한 이유로 국립국어원에서도 무엇을 기준으로 하느냐에 따라 두 가지로 의미를 해석할 수 있다고 답변을 한 것이죠.
문제는 서로 다른 A, B가 있을 경우, A=B가 되도록 변화시키는 방법에 있습니다. 예를 들어, 두 수 2와 3을 두고 이 둘을 같도록 만들고 싶다면 2에다가 1을 더할 수도 있지만, 3에다가 1을 빼는 방법도 있죠. 즉, 본 문제에서는 어제와 내일이 같아지도록 하는 결과만 제시했지, 어떤 과정을 통해 '어제=내일'이 되도록 하는지에 대한 설명이 없었기 때문에 이중적인 의미를 가지게 된 겁니다.
예를 들어볼까요? 친구 중에 키가 커서 부러운 친구가 있다고 가정합시다. 그와 같은 키가 되고 싶어서 친구에게 이렇게 말합니다.
"너의 키가 나의 키였으면 좋겠다."
그런데 이렇게 말할 수도 있죠.
"나의 키가 너의 키였으면 좋겠다."
두 문장 모두 문법상으로 전혀 이상할 게 없습니다. 그리고 이런 식으로 만 말했다면 듣는 친구 입장에서는 자신의 키가 오히려 작아지기를 바라는 것으로 오해할 수도 있는 거죠.
결국, "어제가 내일이었으면 좋겠다"와 "내일이 어제였으면 좋겠다"는 본질적으로 같은 문장이며 이 결과를 만드는 방법이 두 가지가 존재할 뿐입니다.
그 외의 반박 주장으로는 문장의 시제가 있습니다. 문제에서는 "어제가 내일이었으면 좋겠다"와 같이 과거형을 쓰고 있죠. 따라서 과거로 돌아가기를 바라는 문장이지 미래로 가기를 바라는 문장이 아니라고 주장하기도 합니다.
그러나 현재 국어 문법에는 바라는 것을 표현하는 시제에 대한 제약 조건은 없습니다. 예를 들어 "돈을 많이 벌면 좋겠다"와 "돈을 많이 벌었으면 좋겠다."는 본질적으로 아무런 차이가 없죠.
● 'A가 B였으면 좋겠다'가 중의적으로 해석되는 이유 (2024.09.11)
주기적으로 SNS에서 이슈가 되는 문제이다 보니 제 글에서도 반박 댓글이 꽤나 많이 달렸습니다. 역시나 가장 많은 반박은 어제를 내일로 옮길 수는 있어도 내일을 어제로 옮긴다는 의미에는 동의할 수 없다는 내용인데요. 이 부분에 대해 좀 더 자세히 설명을 해보겠습니다.
다음 수식을 읽을 때 뭐라고 읽으시나요?
$1+1=3$
모든 분들이 아마 "1 더하기 1은 3이다."라고 읽을 것이라 생각됩니다. 실제로도 이렇게 읽는 것에는 아무런 문제가 없죠.
마찬가지로 다음의 수식도 "A는 B이다."라고 읽습니다.
A$=$B
그리고 여기서 조사만 '은/는'에서 '이/가'로 바꾸면 다음과 같습니다. 물론 뜻을 나타내는 데는 아무런 이상이 없습니다.
| $1+1=3$ | 1 더하기 1이 3이다. |
| A$=$B | A가 B이다. |
결국 "A가 B였으면 좋겠다"는 다음과 같은 말입니다.
A$=$B였으면 좋겠다.
그리고 이것은 다음과 같이 A와 B가 자리를 바꾸어도 그 뜻은 유지됩니다.
| A가 B였으면 좋겠다. | |
| $\Rightarrow $ | A$=$B였으면 좋겠다. |
| $\Rightarrow $ | B$=$A였으면 좋겠다. |
| $\Rightarrow $ | B가 A였으면 좋겠다. |
여기에 반대 입장을 가진 분들도 계시겠지만 여기까지가 현재 정해진 기준이고 국립국어원의 입장과 같습니다.
그럼 이제부터 여기에 예시를 넣어보겠습니다. 먼저 위에서 제시한 예시를 한 번 더 쓰면
"나의 키가 너의 키였으면 좋겠다."
"너의 키가 나의 키였으면 좋겠다."
여기서 실제 나의 키는 160cm이고 너의 키는 180cm라고 가정해 봅시다. 즉, '나의 키=160'이고 '너의 키=180'입니다. 현재 나는 너처럼 키가 컸으면 좋겠다고 생각합니다. 그래서 '너의 키=180'을 위의 문장에 대입하여 다음과 같이 말합니다.
"나의 키가 180이었으면 좋겠다."
"180이 나의 키였으면 좋겠다."
어떤가요? 첫 번째 문장이야 말할 것도 없지만 두 번째 문장처럼 말해도 어색하거나 이해가 안 될 것이 없습니다. 만약 바뀌는 대상을 주어로만 한정한다면 두 번째 문장은 180을 나의 키로 바꾼다는 뜻이 되므로 나의 키가 커지는 게 아니라 180이라는 수 자체의 의미가 160짜리 키를 뜻하는 것으로 바뀐다는 것으로 해석되어야 합니다. 물론 이 해석이 틀린 해석은 아니지만 이런 부자연스러운 해석 외에 다른 해석은 할 수 없게 되는 거죠. 즉, 본 문제가 일요일만 답이고 수요일이 오답이 되어야 한다면 일상에서 "180이 나의 키였으면 좋겠다."와 같은 표현은 허용할 수 없게 됩니다. 즉, 나의 키가 180으로 바뀌었으면 좋겠다는 의미로는 사용할 수 없게 되는 거예요.
이 정도 예시로도 충분하겠지만 좀 더 들어볼게요. 학교에서 아이들이 흔히 할 수 있는 말이죠.

"우리 반 담임쌤이 차은우였으면 좋겠다."
"차은우가 우리 반 담임이었으면 좋겠다."
두 문장에 괴리감이 느껴지시나요? 둘 다 너무나 자연스럽게 할 수 있는 말이죠. 그런데 만약 현재의 담임 선생님이 호랑이 선생님이라면 이 문장은 담임을 차은우로 바꾸고 싶다는 뜻뿐만 아니라 차은우를 담임선생님으로 바꾼다는 뜻도 함께 가집니다. 그런데 현재의 담임은 호랑이 선생님이죠. 즉, 차은우가 호랑이 선생님으로 바뀌길 바란다는 뜻이 됩니다. 따라서 이런 문장에서 바뀌는 대상을 주어로만 한정해야 한다면 두 번째 문장은 이런 이상한 해석밖에 할 수 없게 되는 겁니다.
내 얼굴이 예뻐지길 바라는 마음에서 다음과 같이 말했다고 가정해 봅시다.
"딱 하루만이라도 내 얼굴이 장원영 얼굴이었으면 좋겠다."
"딱 하루만이라도 장원영 얼굴이 내 얼굴이었으면 좋겠다."
두 번째 문장처럼 말했다고 해도 앞뒤 문맥을 통해서 내 얼굴이 장원영 얼굴로 바뀌기를 바라는 마음에서 한 얘기라는 건 누구나 이해할 수 있습니다. 물론 두 문장 모두 장원영 얼굴을 내 얼굴로 바꾼다는 뜻도 가지고 있어요. 즉, 두 가지 뜻으로 해석될 수 있으므로 앞 뒤 문맥을 따져봐서 어떤 뜻으로 말한 것인지 추론을 해야 합니다.
그럼 이제 생각해 봅시다. "A가 B였으면 좋겠다"는 중의적으로 해석되는 말이라 상황에 따라 그 뜻을 이해하기에 불편함이 있을 수는 있습니다. 그렇다면 이런 불편함을 없애기 위해서 이런 문장을 한쪽으로만 해석되도록 규정을 바꾸면 어떻게 될까요? 이것은 사람마다 입장의 차이가 있을 수는 있습니다. 그러나 우리는 일상에서도 "이제부터 나의 임무는 ~이다." 대신 "이제부턴 ~(이)가 나의 임무이다."와 같은 말을 흔히 사용할 수 있습니다. "이제부터 내 최애 음식은 ~이다." 대신 "이제부턴 ~(ㅇ)가 내 최애음식이다."와 같은 말을 흔히 사용할 수 있습니다. '어제가 내일이었으면 좋겠다'와 같은 이상한 문제에 명확한 답을 내리기 위해 이런 표현들을 표준어에서 전부 빼버리는 게 과연 옳을까요?
언어는 다양한 표현 방식을 위해 허용범위를 넓히는 경우는 있어도 허용범위를 제한하도록 바꾸는 경우는 없습니다. '너무'라는 단어는 과거엔 부정적인 의미로만 허용되었지만 일상에서 "너무 예쁘다"와 같은 표현을 많이 쓰다 보니까 그 뜻을 일반적인 기준을 넘어선다는 뜻으로 폭넓게 해석해서 긍정적인 상황에서도 쓸 수 있도록 바뀌었죠. 이런 일을 담당하는 곳이 국립국어원이고 여기서 정한 기준이 국가 언어의 표준이 됩니다. 'A가 B이다'를 한쪽으로 해석하도록 제한해 버린다면 "장원영 얼굴이 내 얼굴이었으면 좋겠다."와 같은 표현은 내 얼굴이 바뀌기를 바라는 뜻으로는 사용할 수 없게 됩니다. 그리고 다음과 같은 웃기는 상황이 벌어질 수도 있겠죠.
"여태까지 제 마음속 1순위는 A였지만, 이젠 당신이 제 마음속 1순위예요."
"그 표현은 틀렸어요. 주어가 당신이므로 이건 님의 마음속 1순위를 바꾸는 게 아니라 나를 A로 바꾼다는 뜻이라서 기분이 나쁘네요. 그러니까 어순을 그렇게 하지 말고 '제 마음속 1순위는 당신이에요'라고 고쳐서 말해주세요. 이런 기본적인 것까지 하나하나 짚어줘야 합니까?"
● 결론
제 블로그의 수학 이슈 카테고리에서 각종 논란이 되는 문제를 주제로 포스팅을 쓰면서 같은 결론을 내린 적이 있었는데, 이번 문제의 논란도 결국은 문제 의도의 애매함입니다. 복수 정답을 의도한 것이라면 몰라도 단일 정답을 의도한 거라면 출제 오류가 됩니다. 결국 출제자가 출제 의도를 명확하게 표현하지 못한 탓이죠. 문제적 남자에 방송됐을 당시에는 논란을 피하기 위해 보기에서 수요일을 빼고 출제했습니다.

그러나 사실 이것도 적절치 못한 출제입니다. 만약 학교 수학 시험에서 답이 두 개가 나오는 문제인데 그중에 하나만 보기에 제시했다면 해당 문제는 정답 없음으로 처리되어 재시험을 봐야 할 수도 있습니다. 왜냐? 어떤 학생은 답 두 개를 모두 구했는데 보기에는 모두를 반영한 적절한 답이 없어서 답을 못 찍는 일이 발생할 수도 있으니까요.
결론: 문제를 만들 때는 논란이 발생하지 않도록 의도와 조건을 충분하고도 치밀하게 제시해야 합니다.

'수학 이슈' 카테고리의 다른 글
| 안 풀리는 뇌 정지 수학 문제 (970원, 돈 계산, 산수, 사칙 연산) (0) | 2023.04.24 |
|---|---|
| 여러 가지 두뇌 회전 퀴즈 (수학, 단어 연상, 숨은 그림) (0) | 2023.04.13 |
| Study=Fail? 공부하면 안 되는 이유 + 반박 (수학 이슈) (4) | 2022.07.23 |
| 전국의 수학선생님이 알아두셔야 할 서술형에서 상위 개념으로 푼 학생에 대한 대처 방법 ('8×7+17=73' 오답 처리 논란) (2) | 2022.07.10 |
| 페북에서 난리난 초등학교 수학 분수 3/4 문제 논란 (학원강사 vs 수학교사) (8) | 2022.06.04 |





댓글 영역