고정 헤더 영역
상세 컨텐츠
본문
2024학년도 수능 수학 22번 정답률 1.4% 킬러 문항의 쉽고 자세한 해설 (공통 미적분 고난도 문제 쉬운 풀이)


안녕하세요? holymath입니다. 늦었지만 수험생 여러분 모두 수고 많으셨고 남은 입시 준비도 잘 되어서 좋은 결과가 있기를 바랍니다.
수학에서 킬러 문항에 대한 얘기로 난리가 났습니다. 수능에서 킬러 문항을 배제한다고 해놓고 정답률이 1.4%에 달하는 초고난도 문항이 출제된 건데요. 문제가 된 킬러 문항은 공통 영역의 마지막 주관식 문항인 22번입니다. 도대체 어떤 문항이길래 이렇게 화제가 되었는지 한 번 풀어보았습니다.

● 문항 의도 분석
우선 네모 박스에 당황스러운 조건이 들어있습니다. 정수 $k$를 사이에 두고 양쪽 정수인 $k-1$과 $k+1$에서의 두 함숫값 $f(k-1)$, $f(k+1)$에 대하여 $f(k-1)f(k+1)<0$인 경우가 없다고 합니다. 즉, 두 함숫값의 부호가 달라지는 일이 존재하지 않는다고 하는데요. 대부분의 킬러 문항은 특별한 그래프 모양을 이루도록 조건을 주고 그 함수가 무엇인가를 추론하는 경우가 많죠. 이 문제도 뭔가 특별한 모양의 그래프가 되도록 추론해야 하는 유형으로 보이는데 당장은 이 조건을 분석하기에 굉장히 어려워 보이니 다른 조건도 한 번 살펴보겠습니다.
문제의 서두를 보면 최고차항의 계수가 $1$인 삼차함수라고 되어있네요. 이런 삼차함수라면 그래프의 유형은 다음의 두 가지로 압축된다는 건 공부를 어느 정도 해보면 다들 알 수 있어요.
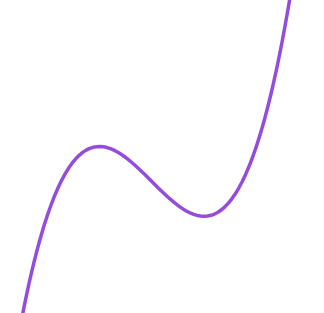
| <유형 1> | <유형 2> |
 |
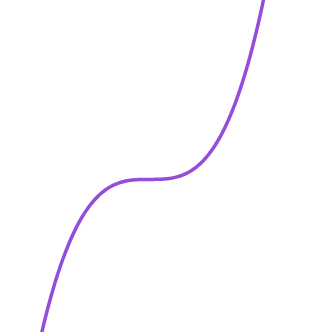 |
첫 번째 유형은 서로 다른 두 개의 극값을 기준으로 그 사이의 구간에서만 함숫값이 감소하고 나머지 구간에서는 함숫값이 증가하는 형태예요. 두 번째 유형은 극값이 존재하지 않고 실수 전체의 구간에서 함숫값이 증가하는 형태입니다.
그럼 이제 문제 뒷부분의 조건을 봅시다. 다음 조건을 통해 구하고자 하는 함수가 어떤 유형인지는 파악할 수 있습니다.
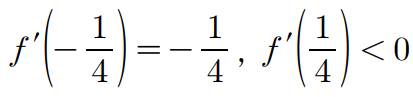
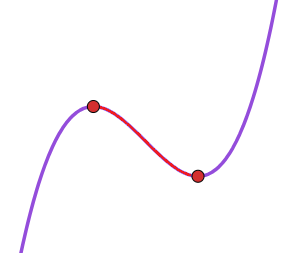
바로 첫 번째 유형이 되겠죠. 두 번째 유형은 미분계수가 항상 $0$ 이상이 되기 때문입니다. 그리고 위의 조건에 의해 두 점 $(-\frac{1}{4},~f \left (-\frac{1}{4} \right ))$, $(\frac{1}{4},~f \left (\frac{1}{4} \right ))$은 그림에서 빨간색으로 칠한 그래프 위에 존재하게 됩니다. 저 구간에서만 함숫값이 감소하니까요.
● x축과의 위치 및 교점의 좌표
여기까지는 무난하게 접근할 수 있죠. 이제 문제의 핵심 조건인 네모 박스 내용으로 들어가 봅시다.

이 조건을 통해 의도한 그래프를 추론했는가가 이 문제를 푸는지 못 푸는지를 결정합니다. 거리가 2만큼 떨어진 두 정수에서 함숫값을 비교해 봤을 때 두 함숫값의 부호가 서로 반대인 경우는 없다. 즉, 한 점은 $x$축 위에 있고 한 점은 $x$축 아래에 놓이는 경우가 없다는 것을 의미하죠. 그렇다면 이것으로 추론해 볼 수 있는 것은 "$x$축 근방에서 그래프가 어떤 식으로 형성되어 있는가?"입니다.
문제의 함수는 삼차함수이므로 그래프가 $x$축을 지나는 부분이 반드시 존재하죠. 그런데 예를 들어 두 정수 $k-1$, $k+1$을 사이에 두고 그래프가 다음과 같이 증가하면서 $x$축을 뚫고 지나갈 경우 $f(k-1)f(k+1)<0$이 되어 네모박스의 조건을 못 지키게 됩니다.
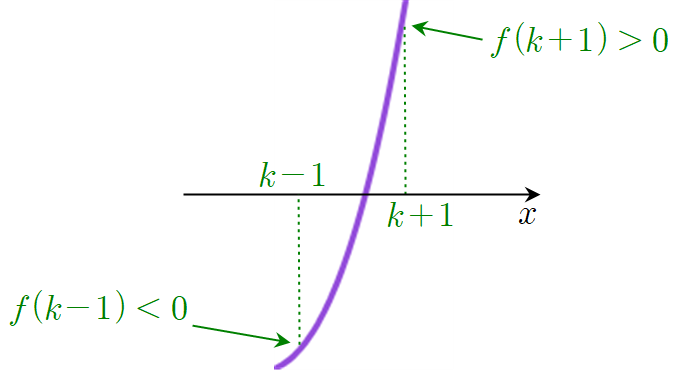
따라서 그래프가 $x$축과 교차하는 지점에서 $f(k-1)f(k+1)\geq 0$의 조건을 지키려면 그래프가 계속해서 올라갈 것이 아니라 다음과 같이 $x$축과의 두 교점 사이의 거리가 $1$을 넘지 않도록 그래프가 다시 꺾여야 합니다. 만약 두 교점 사이의 거리가 벌어져서 $k+1$에서의 함숫값이 양수가 되기라도 하면 $f(k-1)f(k+1)<0$가 되고 $k$에서의 함숫값이 양수가 된다면 $f(k-2)f(k)<0$가 되어 조건을 만족하지 못할 테니까요.
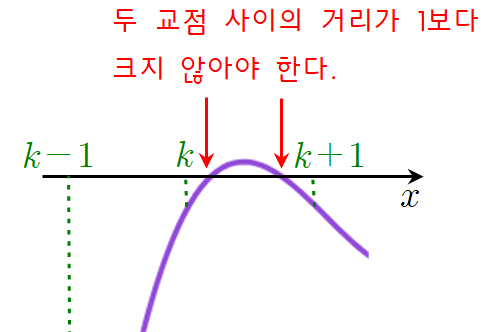
이와 같은 원리는 다음과 같이 그래프가 내려가다가 다시 꺾여서 올라가는 경우에도 마찬가지입니다. 만약 두 교점 사이의 거리가 벌어져서 $k-1$에서의 함숫값이 음수가 되기라도 하면 $f(k-1)f(k+1)<0$가 되고 $k$에서의 함숫값이 음수가 된다면 $f(k)f(k+2)<0$가 되어 조건을 만족하지 못할 테니까요.
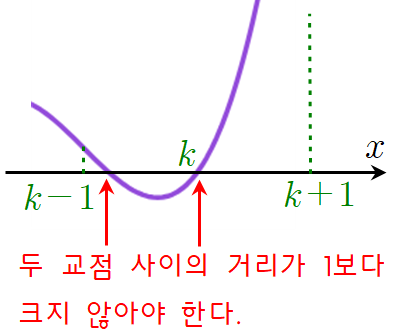
위의 그림처럼 특정 정수에서의 함숫값이 $0$이 된다면 조건을 만족시키기 더욱 유리한 조건이 되겠죠. 위처럼 $f(k)=0$이라면 $f(k-2)f(k)=0$이고 $f(k)f(k+2)=0$이 되어 조건을 모두 만족시킬 수 있습니다.
● 그래프의 개형 추론
이제 구하려는 함수의 그래프의 전체적인 개형으로 돌아가서 접근해 보겠습니다. 앞에서 알아본 조건에 의하면 두 점 $(-\frac{1}{4},~f \left (-\frac{1}{4} \right ))$, $(\frac{1}{4},~f \left (\frac{1}{4} \right ))$은 다음 그림에서 빨간색으로 칠한 그래프 위에 존재합니다. 또한, $-\frac{1}{4}$와 $\frac{1}{4}$ 사이에는 $0$이 있으므로 점 $(0,~f(0))$ 또한 빨간색 그래프 위에 존재합니다. 그리고 위에서 알아본 것처럼 가까운 두 교점 사이의 거리가 1을 넘지 않도록 $x$축이 지나가야 합니다. 이를 위해서는 다음과 같이 $x$축이 빨간색 그래프를 반드시 뚫고 지나가야만 하죠. 즉, (극댓값)$\times$(극솟값)$\leq 0$이 되어야 합니다.
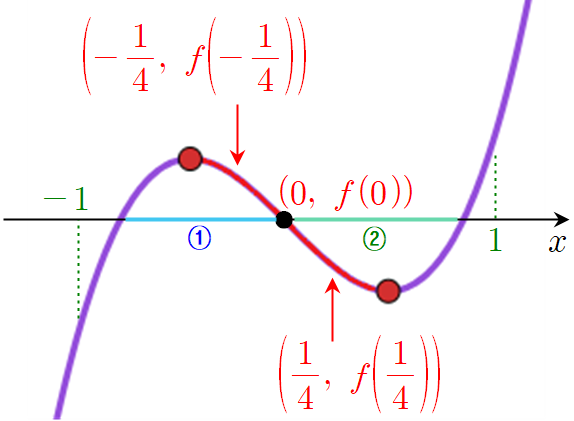
여기서 결정적인 윤곽을 잡을 수 있어요. $x$축에서 원점이 그림에서 ①번 위치에 있게 되면 $f(0)>0$이 되는데 $f(-2)<0$이므로 $f(-2)f(0)<0$이 되어 조건을 만족 못하게 됩니다. 마찬가지로 그림에서 ②번 위치에 있게 되면 $f(0)<0$이 되는데 $f(2)>0$이므로 $f(0)f(2)<0$이 되어 조건을 만족 못하게 됩니다. 따라서 $(0,~f(0))$은 $x$축과의 교점이고 따라서 $f(0)=0$이 됨을 알 수 있습니다.
그렇다면 이제 위의 그림의 그래프 모양으로 윤곽을 완전히 잡았다고 할 수 있을까요? 아직 고려할 게 하나 남았습니다. 위의 그래프 모양대로라면 $f(1)>0$이고 $f(-1)<0$이므로 $f(-1)f(1)<0$이 되어 조건을 만족 못하게 됩니다. 그렇다고 $-1$이 ①번 위치에 있거나 $1$이 ②번 위치에 있게 되면 $f(-3)$이나 $f(3)$에 의해 역시 조건을 만족 못하게 돼요. 따라서 모든 조건이 완벽하게 맞아떨어지기 위해서는 $f(-1)=0$ 또는 $f(1)=0$이 반드시 만족이 되어야 합니다.
위에서 알아본 모든 조건을 정리했을 때, 함수 $f(x)$의 수식은 다음의 두 가지로 축약할 수 있습니다. 참고로 $f(-1)=0$과 $f(1)=0$이 모두 성립하는 경우에는 $f(x)=x(x-1)(x+1)=x^3-x$가 되는데 이 경우 $f'(x)=3x^2-1$이 되어서 $f'(-\frac{1}{4})=-\frac{1}{4}$을 만족하지 않아요. 따라서 둘 중 하나만 성립합니다.
| 구분 | $f(-1)=0$인 경우 | $f(1)=0$인 경우 |
| 그래프 개형 |
 |
 |
| 함수식 | $f(x)=x(x+1)(x-k)$ | $f(x)=x(x-1)(x+k)$ |
| $k$ 범위 | $0<k<1$ | |
● 풀이 및 정답
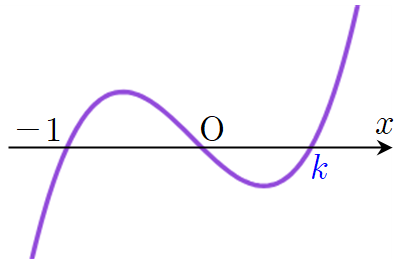
1) $f(x)=x(x+1)(x-k)$ 인 경우
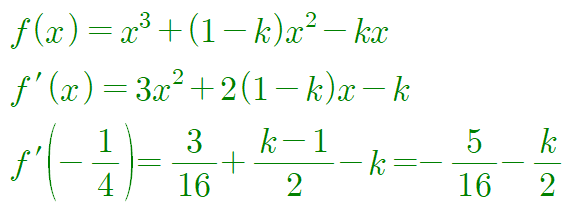
여기서 $k>0$이므로 다음이 성립하여 조건을 만족하지 못합니다.
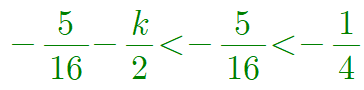
2) $f(x)=x(x-1)(x+k)$ 인 경우
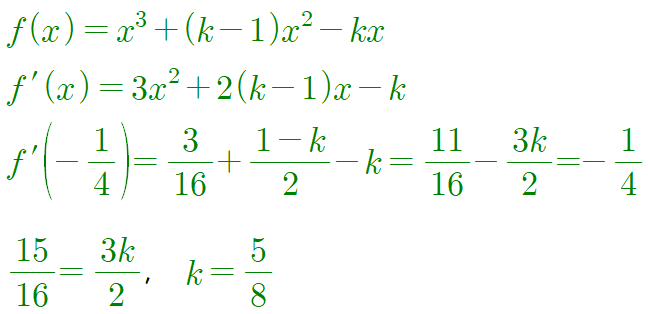
그리고 이 경우 다음과 같이 $f'\left (\frac{1}{4}\right )$이 음수라는 조건까지 만족시킵니다.
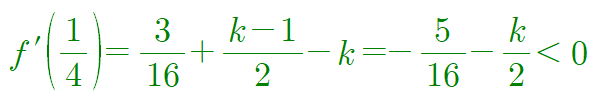
1), 2)로부터 구하는 함수 및 $f(8)$의 값은 다음과 같습니다.
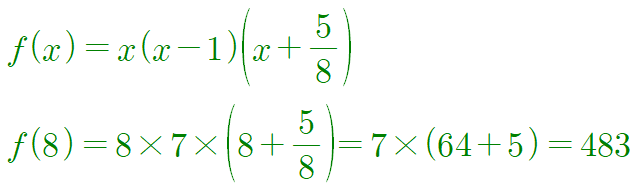
보다시피 수식 계산이 크게 복잡하진 않아서 출제 및 검토 위원 입장에서는 함수 추론만 잘하면 충분히 풀 수 있는 문제이니 킬러 문항은 아니라고 생각했을지도 모르겠네요. 그들의 입장을 최대한 너그럽게 생각한다면요. 그런데 정수 조건으로부터 사실상 킬러 문항과 다름없는 생각과 탐구를 해야 하니, 어느 때보다도 긴장하면서 푸는 수험생 입장에선 결코 만만한 문제가 아니었을 것 같습니다. 이 문제를 맞히신 1.4%의 수험생들에게 박수를 보냅니다.

♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.
'수능·모의고사 문제 해설' 카테고리의 다른 글
| 2023학년도 수능 9월 모의고사 수학 영역 기하 29, 30번 해설 (2022.08.31 시행) (2) | 2022.09.04 |
|---|---|
| 2023학년도 수능 9월 모의고사 수학 21, 22번 해설 (2022.08.31 시행) (8) | 2022.09.01 |
| 2023학년도 수능 9월 모의고사 수학 영역 미적분 29, 30번 해설 (2022.08.31 시행) (8) | 2022.08.31 |





댓글 영역