고정 헤더 영역
상세 컨텐츠
본문
2023학년도 수능 9월 모의고사 수학 영역 기하 29, 30번 해설 (2022.08.31 시행)

안녕하세요? holymath입니다. 이번 포스팅에서는 2023학년도 대학수학능력시험 9월 모의평가 수학에서 기하 29번, 30번 문제를 해설해보겠습니다. 공통영역부터 해서 전반적으로 계산이 복잡하거나 긴 문제는 없었던 것 같습니다. 예전의 초고난도 문제를 풀 때는 문제 아래의 여백뿐만 아니라 겉표지의 여백까지 필요한 경우도 많았는데 요즘의 문제는 점점 아이디어가 중요해지는 쪽으로 변해가는 것 같습니다. 특히 기하 문제는 더욱 그런 거 같네요.

● 기하 29번 문제 해설

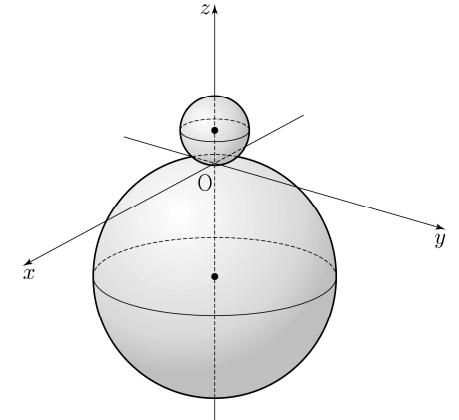
3차원에서 생각하면 머리도 아프고, 우리가 풀고 있는 문제지는 2차원 면이라서 여백에 공간을 완벽하게 구현할 수가 없습니다. 공간도형, 공간좌표 문제의 핵심은 복잡한 공간을 단순화 시키는 거예요. 즉, 3차원을 2차원의 시각으로 바라보는 거죠.
이 문제에서의 핵심은 $zx$ 평면입니다. 점 A를 지나고 $zx$ 평면에 수직인 평면 $\alpha $를 가정했죠. 구 $S_2$가 평면 $\alpha $와 만나서 생기는 원 $C$ 역시 평면 $\alpha $의 일부이므로 $zx$ 평면에 수직이에요.
그리고 원 $C$ 위의 점 중 $z$ 좌표가 최소인 점을 B라 하였으므로 점 B 역시 $zx$ 평면 위에 존재합니다. 그렇다면 두 구 $S_1$, $S_2$의 중심을 각각 $\textrm{O}_1$, $\textrm{O}_2$라 했을 때, 점 B에서 구 $S_2$와 접하는 평면 $\beta $는 구 $S_2$의 반지름인 선분 $\textrm{BO}_2$ 와 수직이므로 평면 $\beta $ 또한 $zx$ 평면에 수직입니다.
결국 평면 $\alpha $와 $\beta $랑 원 $C$ 모두 $zx$ 평면에 수직이므로 이 문제는 다음과 같이 $zx$ 평면을 문제지 위에 바닥으로 놓고 접근하면 됩니다.
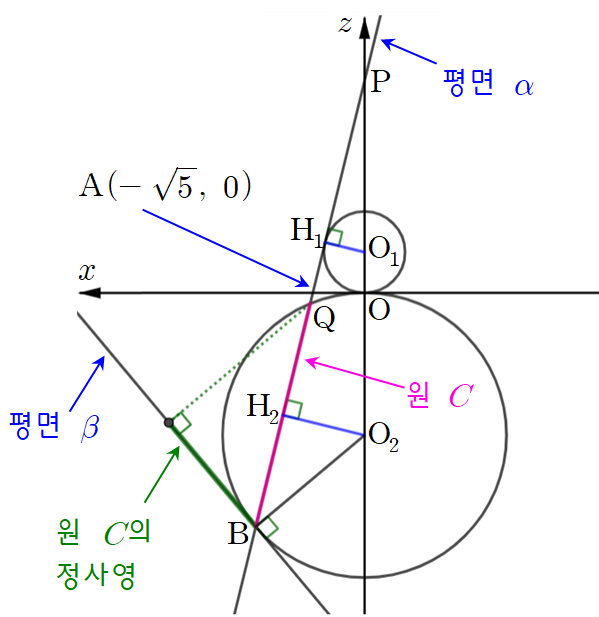
이렇게 $y$축의 음의 방향으로 평면 $zx$를 바라보면 평면 $\alpha $, $\beta $ 및 원 $C$가 모두 직선이나 선분 모양이 됨을 알 수 있어요. 그럼 이 문제는 평면 위의 원의 방정식 문제로 접근하면 되므로 두 구 $S_1$, $S_2$를 각각 원 $C_1$, $C_2$로 놓은 다음 편의상 점 $\textrm{A}$의 좌표를 $(-\sqrt{5},~0)$으로 놓고 풀이를 시작할 겁니다. 위의 평면을 $xy$ 평면처럼 가정하고 푸는 거죠.
이제 점 $\textrm{A}$를 지나고 원 $C_1$에 접하는 접선을 구하기 위해 다음과 같이 방정식을 세웁니다.
$y=m(x+\sqrt{5})$, $mx-y+\sqrt{5}m=0$
이 직선과 $C_1$의 중심 $\textrm{O}_1(0,~2)$과의 거리가 반지름인 2와 같아야 하므로
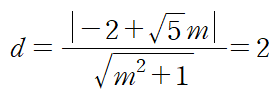
$m$을 구하기 위해 방정식을 풀면
$5m^2-4\sqrt{5}m+4=4m^2+4$
$m^2-4\sqrt{5}m=0$
기울기 $m$은 0이 아니므로 $m=4\sqrt{5}$입니다.
따라서 접선의 방정식은 $4\sqrt{5}x-y+20=0$이고 이 직선과 $C_2$의 중심 $\textrm{O}_2(0,~-7)$까지의 거리는
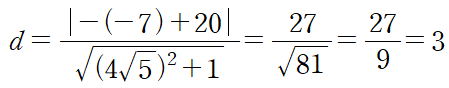
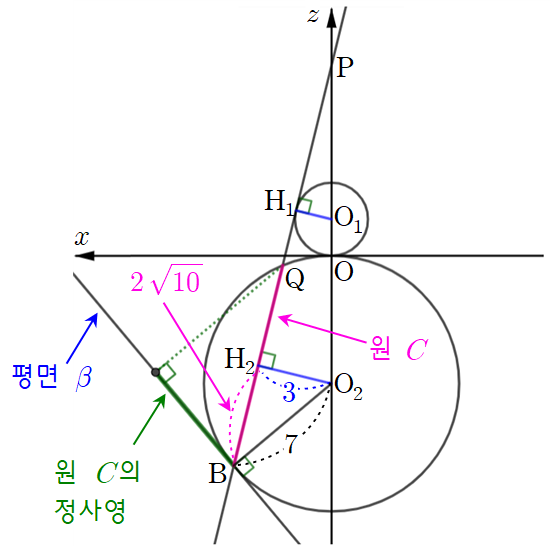
따라서 위의 그림에서 $\overline{\textrm{O}_2\textrm{H}_2}=3$이므로 직각삼각형 $\textrm{BO}_2\textrm{H}_2$에서 피타고라스 정리에 의해 $\overline{\textrm{BH}_2}=2\sqrt{10}$임을 알 수 있어요.
이 길이가 바로 원래 공간에서 원 $C$의 반지름의 길이가 됩니다. 따라서 원 $C$의 넓이는 $40\pi $가 되죠.
이제 정사영의 넓이만 구하면 돼요. 원 $C$와 평면 $\beta $사이의 각을 구해야 되는데 이 각 또한 다음과 같이 평면에서의 직선 사이의 각 처럼 구하면 됩니다.
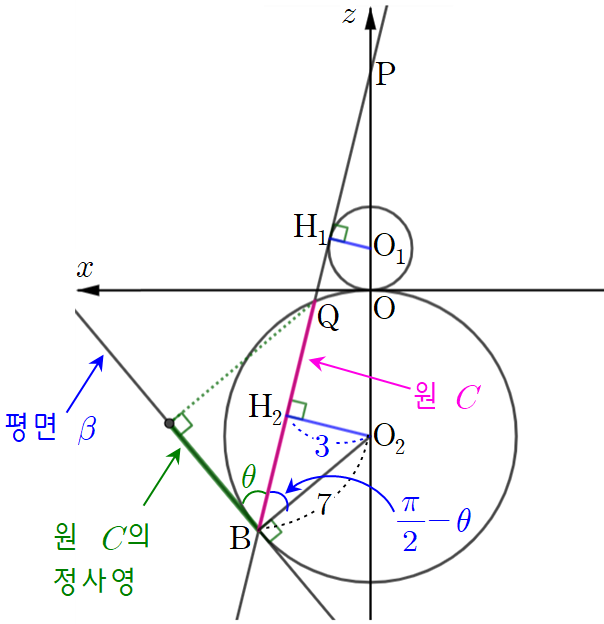
위의 그림과 같이 원 $C$와 평면 $\beta $사이의 각을 $\theta$라 하면 $\angle \textrm{H}_2\textrm{BO}_2=\frac{\pi }{2}-\theta $이죠. 그럼 다음과 같이 정사영의 넓이를 구할 수 있습니다.
$40\pi \times \textrm{cos}\theta =40\pi \times$ $\textrm{sin}(\frac{\pi }{2}-\theta)$
$=40\pi \times \frac{3}{7}=\frac{120}{7}\pi $
따라서 $p+q=120+7=$ $127$입니다.
● 기하 30번 문제 해설

문제의 첫 조건 $(\left|\overrightarrow{\textrm{AX}} \right|-2)(\left|\overrightarrow{\textrm{BX}} \right|-2)=0$을 풀면 다음과 같습니다.
$\left|\overrightarrow{\textrm{AX}} \right|=2$ 또는 $\left|\overrightarrow{\textrm{BX}} \right|=2$
'또는'으로 연결되어 있으므로 점 $\textrm{X}$는 각 점 $\textrm{A}$, $\textrm{B}$를 중심으로 하고 반지름의 길이가 2인 두 원 중 하나에 존재합니다.
그런데 조건 $\left|\overrightarrow{\textrm{OX}} \right|\geq 2$부터 점 $\textrm{X}$는 원점을 중심으로 하고 반지름의 길이가 2인 원의 내부에는 존재할 수 없습니다.
따라서 이 조건을 종합하면 점 $\textrm{X}$가 그리는 도형을 실선으로 나타내면 다음과 같습니다.
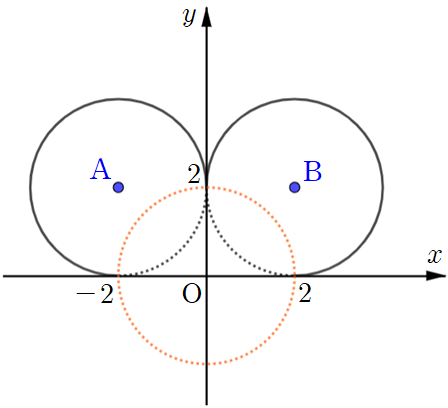
이렇게 생긴 도형 위에 두 점 $\textrm{P}$, $\textrm{Q}$가 존재하는 상황이죠. 이제 네모 안의 조건을 보겠습니다.
(가) 조건의 경우 복잡하게 식을 뜯어봐야 할 것 같이 생겼지만 사실은 단순한 원리예요. 두 내적 값의 곱이 0 이상이라는 것은 둘 중 하나가 0이거나 부호가 같아야 한다는 뜻이죠. 즉, 두 벡터 $\overrightarrow{\textrm{OP}}$, $\overrightarrow{\textrm{OQ}}$는 단위벡터 $\overrightarrow{u}$와 이루는 각이 둘 다 예각이거나 둘 다 둔각이 되어야 한다는 겁니다. 즉, 두 점 $\textrm{P}$, $\textrm{Q}$는 둘 다 제1사분면에 있거나 둘 다 제2사분면에 있거나 누군가가 $y$축 위에 있는 상황이라고 이해할 수 있습니다.
(나) 조건은 두 점 $\textrm{P}$, $\textrm{Q}$ 사이의 거리가 2로 고정이라는 뜻이죠.
즉, 두 조건을 종합하면 두 점 $\textrm{P}$, $\textrm{Q}$는 거리가 2만큼 떨어져 있으면서 하나의 원호 위에 존재합니다. 그렇다면 원점에서 두 점까지 이르는 거리 또한 2로 같으므로 결국 다음과 같이 삼각형 $\textrm{OPQ}$가 정삼각형을 이루는 상황인 거죠.
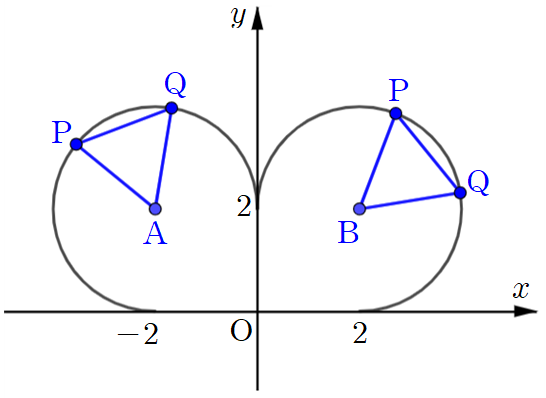
이제 최종 질문을 보면 $\overrightarrow{\textrm{OY}}=\overrightarrow{\textrm{OP}}+\overrightarrow{\textrm{OQ}}$로 정의하고 있어요. 편의상 제2사분면에서 원의 중심을 기준으로 이 식을 분석하면
$\overrightarrow{\textrm{OP}}+\overrightarrow{\textrm{OQ}}=2\overrightarrow{\textrm{OA}}+\overrightarrow{\textrm{AP}}+\overrightarrow{\textrm{AQ}}$
이때, 벡터 $\overrightarrow{\textrm{AP}}+\overrightarrow{\textrm{AQ}}$는 아래 그림에서 자주색 화살표와 같으며 이 벡터의 종점을 $\textrm{Y}'$이라 하면 $\textrm{Y}'$의 자취는 다음과 같이 반지름의 길이가 $2\sqrt{3}$이고 중심각의 크기가 $210^{\circ}$인 원호를 그립니다.
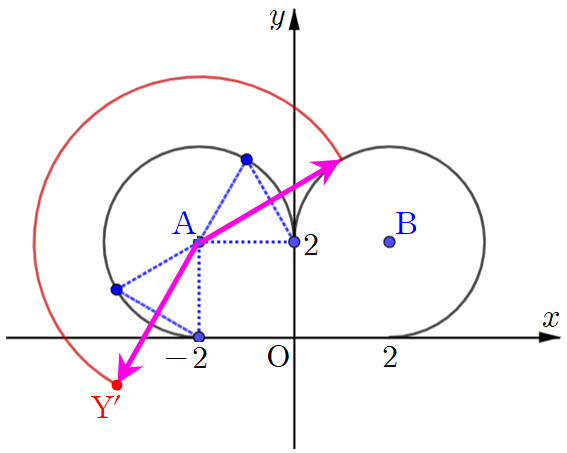
따라서 $\overrightarrow{\textrm{OY}}=2\overrightarrow{\textrm{OA}}+\overrightarrow{\textrm{AP}}+\overrightarrow{\textrm{AQ}}$를 만족시키는 점 $\textrm{Y}$는 중심의 좌표만 $(-4,~4)$로 바뀌고 똑같은 원호를 그려요. 따라서 이 경우 점 $\textrm{Y}$가 그리는 자취의 길이는
$2\times2\sqrt{3}\pi \times \frac{210}{360}$
$=4\sqrt{3}\times \frac{7}{12}\pi=\frac{7}{3}\sqrt{3}\pi$
이런 원리는 점 $\textrm{B}$가 중심인 원 위에서 관찰해도 똑같은 결과가 나오죠. 따라서 점 $\textrm{Y}$가 그리는 자취의 총길이는 $2\times \frac{7}{3}\sqrt{3}\pi= \frac{14}{3}\sqrt{3}\pi$입니다.
따라서 구하는 답은 $p+q=3+14=$ $17$입니다.
♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'수능·모의고사 문제 해설' 카테고리의 다른 글
| 2024학년도 수능 수학 22번 정답률 1.4% 킬러 문항의 쉽고 자세한 해설 (공통 미적분 고난도 문제 쉬운 풀이) (2) | 2023.11.19 |
|---|---|
| 2023학년도 수능 9월 모의고사 수학 21, 22번 해설 (2022.08.31 시행) (8) | 2022.09.01 |
| 2023학년도 수능 9월 모의고사 수학 영역 미적분 29, 30번 해설 (2022.08.31 시행) (8) | 2022.08.31 |





댓글 영역