고정 헤더 영역
상세 컨텐츠
본문
2023학년도 수능 9월 모의고사 수학 영역 21, 22번 해설 (2022.08.31 시행)

안녕하세요? holymath입니다. 어제에 이어 2023학년도 대학수학능력시험 9월 모의평가 수학 영역의 문제를 해설하겠습니다. 오늘은 공통 영역인 21번과 22번을 해설해보겠습니다.

● 수학 21번 문제 해설

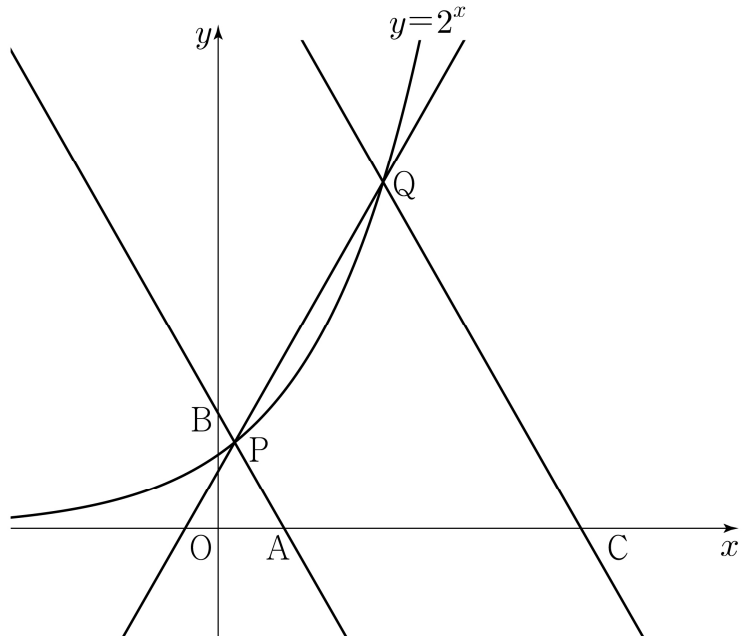
복잡하게 방정식을 세워서 $m$의 값을 찾아내고 답을 구할 수도 있지만 위에서 제시된 비례식으로부터 다음과 같이 보조점과 보조선을 그릴 수 있으면 직선의 방정식을 세우지 않고도 풀 수 있습니다.
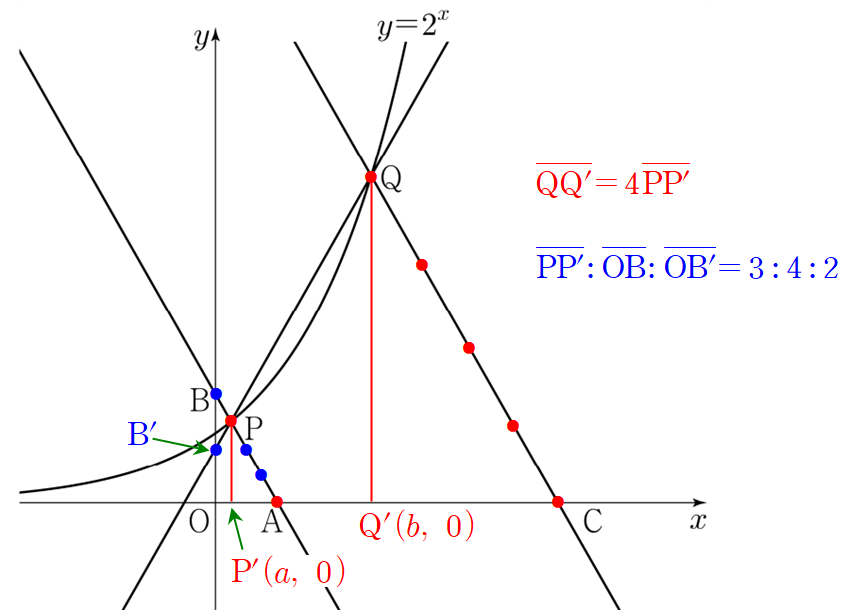
즉, $\overline{\textrm{AB}}=\frac{4}{3}\overline{\textrm{AP}}$이므로 $\overline{\textrm{CQ}}=3\overline{\textrm{AB}}=4\overline{\textrm{AP}}$입니다.
직선 AB와 직선 CQ가 평행하므로 점 P와 점 Q에서 $x$축에 내린 수선의 발을 각각 P', Q'이라 하면 직각삼각형의 닮음비에 의해 $\overline{\textrm{QQ}'}=4\overline{\textrm{PP}'}$임을 유도할 수 있습니다.
따라서 $2^b=4\times 2^a=2^{a+2}$이므로 $b=a+2$임을 알 수 있어요.
또한, 직선 PQ와 $y$축이 만나는 점을 B'이라 하면
$\overline{\textrm{PP}'}:\overline{\textrm{OB}}:\overline{\textrm{OB}'}=3:4:2$
라는 사실 또한 유도할 수 있습니다.
따라서 점 $\textrm{B}'$의 좌표는 $(0,~\frac{2}{3}\times 2^a)$입니다.
이제, 세 점 $\textrm{B}'$, $\textrm{P}$, $\textrm{Q}$가 한 직선 위에 있다는 사실을 이용하여 기울기를 구하면
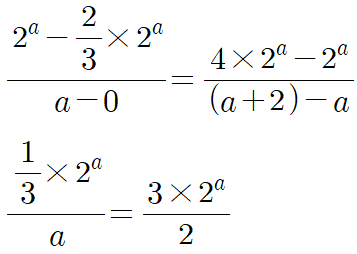
분자끼리 비교했을 때 우변의 분자가 좌변의 분자의 9배이므로 이것을 분모에도 적용하면
$9a=2$, $a=\frac{2}{9}$
따라서 $b=\frac{2}{9}+2$이므로 구하는 답은 다음과 같습니다.
$90\times (a+b)=90\times (\frac{4}{9}+2)$
$=40+180=$220
● 수학 22번 문제 해설

그동안 출제했던 보스급 주관식 문제와 유사합니다. 삼차함수 $f(x)$를 가지고 특정 값 $t$를 기준으로 함수를 비틀어서 새로운 함수를 만들죠. 그리고 이 함수가 갖는 특징을 이용하여 원래의 함수를 추론하는 방식입니다.
우선 삼차함수 $f(x)$의 최고차항의 계수가 1이고 $x=3$에서 극댓값 8을 갖는다는 사실로부터 $y=f(x)$의 그래프는 다음과 같은 모양임을 알 수 있습니다.
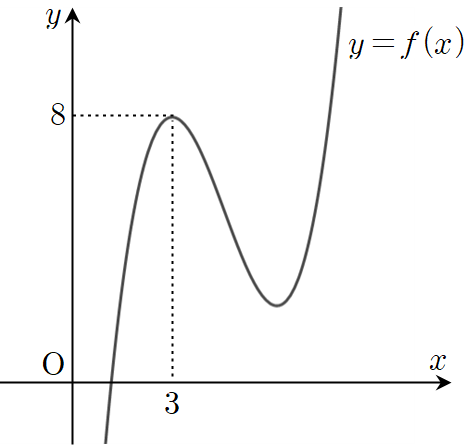
이제 함수 $g(x)$를 탐구해보면 $x<t$인 경우 $y=f(x)$를 $y$축에 대하여 대칭이동 시킨 다음 $y$축의 방향으로 $2f(t)$만큼 평행이동시킨 그래프가 되죠.
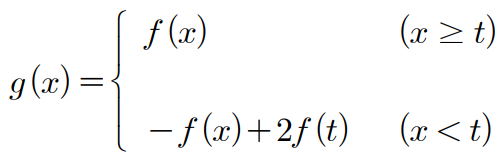
그런데 식 $-f(x)+2f(t)$와 원래의 식 $f(x)$를 비교해보면 두 식의 평균이 $f(t)$가 된다는 걸 알 수 있습니다. 이 말이 무엇이냐? 다음과 같이 $y=f(x)$의 그래프 위의 점 $(t,~f(t))$에 대하여 $x<t$인 영역의 그래프를 직선 $y=f(t)$에 대하여 대칭이동시킨 그래프가 바로 $y=g(x)$의 그래프가 된다는 겁니다.
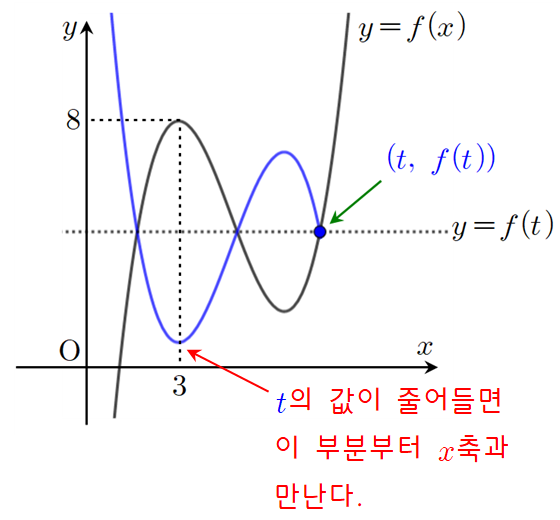
그렇다면 이제부터 점 $(t,~f(t))$를 어디에 위치시키느냐에 따라 $y=g(x)$의 그래프가 어떻게 될지를 파악하셔야 하는데 이 과정에서 머리가 좀 아플 겁니다. 이때, $t$를 충분히 큰 값에서부터 잡고 그 값을 줄여가면서 관찰하는 것이 좋습니다. 그러면 위의 그림처럼 파란색 그래프가 $x$축과 만나지 않으므로 방정식 $g(x)=0$의 실근이 없죠. 따라서 $h(t)=0$입니다.
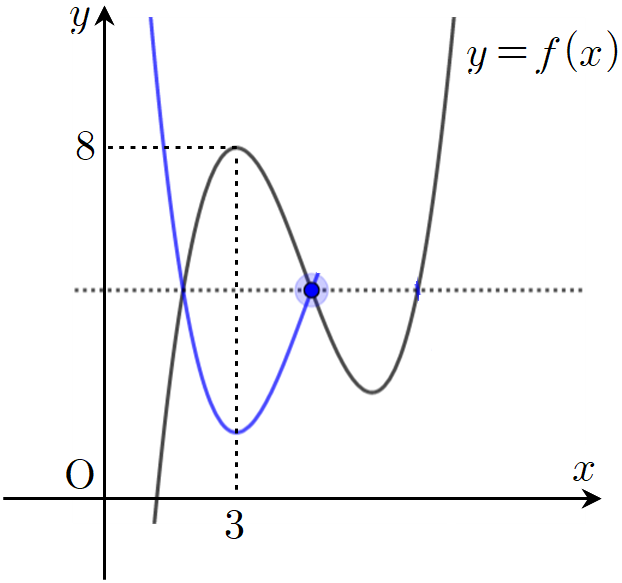
이제 $t$의 값을 천천히 줄여보면 직선 $y=f(t)$와 극대점인 $(3,~8)$ 사이의 거리가 점점 커지므로 $y=g(x)$의 그래프는 $x=3$인 지점에서부터 $x$축과 만나기 시작할 겁니다. 그러면 $h(t)$의 값은 0이었다가 특정 순간에 1이 되고 $y=g(x)$의 그래프가 $x$축 아래까지 침범하면 2로 바뀔 겁니다.
그러다가 점 $(t,~f(t))$가 $y=f(x)$의 극소점을 지나고 극대점 $(3,~8)$을 향해 올라가면 다음과 같이 $y=g(x)$의 그래프는 $x$축과 만나지 않는 순간이 나타납니다. 이 과정에 도달하기까지 $h(t)$의 값은 2에서 특정 순간에 1이 되고 그 순간을 지나면 0이 되는 거죠.
이제 점 $(t,~f(t))$가 극대점 $(3,~8)$을 지난 후에서 한참 동안은 $y=g(x)$의 그래프가 $x$축과 만날 일은 없습니다. 그러다가 언제 다시 만나게 되느냐? 다음과 같이 점 $(t,~f(t))$가 $x$축 위에 도달하는 순간입니다. 이 순간에 $h(t)$의 값은 0에서 순간적으로 1이 되었다가 2가 됩니다.
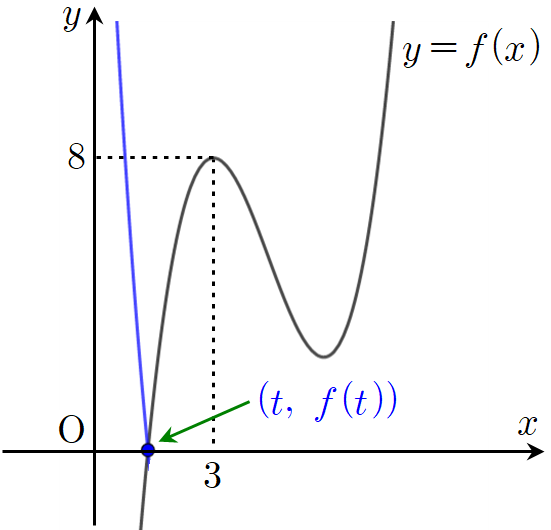
지금까지 과정을 거쳤을 때, $h(t)$가 불연속이 되는 순간이 총 몇 군데인지 세어 보셨나요? 점 $(t,~f(t))$가 $y=f(x)$의 극소점을 지날 때 두 번 불연속이 있었고 여기서 한 번 발생했으므로 총 3번이 되겠죠. 여기서는 $f(x)$의 극솟값이 양수임을 가정하고 조사했는데 만약 극솟값이 음수였으면 불연속이 되는 순간은 더 많았을 겁니다.
그런데 문제에서는 불연속이 딱 두 번만 일어난다고 했죠. 그건 어떤 상황일까요? 위에서처럼 점 $(t,~f(t))$가 $x$축 위를 지날 때는 불연속이 반드시 발생할 수밖에 없죠. 그렇다면 점 $(t,~f(t))$가 $y=f(x)$의 극소점을 지날 때 불연속이 한 번만 일어나도록 해야 한다는 겁니다. 그렇게 되는 경우는 다음과 같이 극솟값이 극댓값 8의 절반인 4가 되는 경우입니다. 이렇게 되면 점 $(t,~f(t))$가 $y=f(x)$의 극소점을 지날 때, $y=g(x)$의 그래프는 $x$축에 잠깐 닿았다가 다시 위쪽으로 움직이므로 $h(t)$의 값은 0에서 잠깐 1이 되었다가 바로 다시 0이 되어 불연속이 한 번만 발생하게 돼요. 참고로 극솟값이 4보다 크다면 이쪽 구간에서는 불연속 자체가 일어나지 않게 되어 $h(t)$는 불연속이 한 번만 존재하게 됩니다.
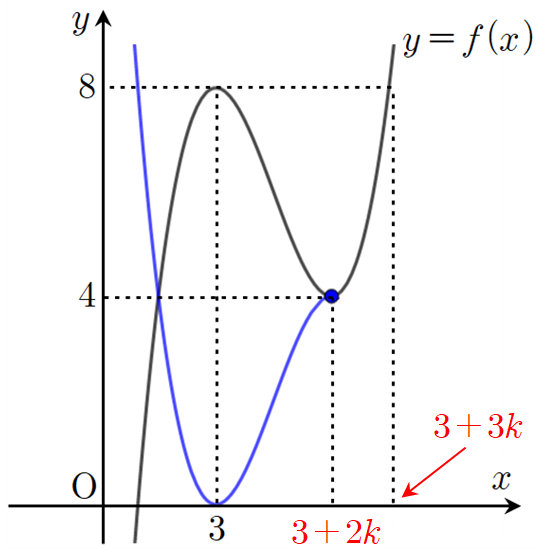
이제 위의 그림을 바탕으로 $f(x)$가 어떤 함수인지 추론할 수 있습니다. 다양한 접근 방법이 있겠지만 $y=f(x)$의 그래프를 $y$축의 방향으로 -8만큼 평행이동하면 $x=3$에서 $x$축과 접하므로 다음과 같이 놓고 시작할 수 있어요.
$f(x)=(x-3)^2\left\{x-(3+3k) \right\}+8$
여기서 삼차함수의 그래프에서 비율을 이용하면 계산을 편리하게 할 수 있어서 그림에서 $f(x)=4$와 $f(x)=8$인 $x$의 값을 각각 $3+2k$, $3+3k$로 놓았음을 참고하세요. 이제 위의 식에다 $f(3+2k)=4$임을 이용해서 값을 대입하면
$f(3+2k)=(3+2k-3)^2\left\{3+2k-(3+3k) \right\}+8$
$=(2k)^2(-k)=-4k^3+8=4$
따라서 $k=1$이므로 $f(x)=(x-3)^2(x-6)+8$입니다.
따라서 $f(8)=5^2\times 2+8=$58입니다.
♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'수능·모의고사 문제 해설' 카테고리의 다른 글
| 2024학년도 수능 수학 22번 정답률 1.4% 킬러 문항의 쉽고 자세한 해설 (공통 미적분 고난도 문제 쉬운 풀이) (2) | 2023.11.19 |
|---|---|
| 2023학년도 수능 9월 모의고사 수학 영역 기하 29, 30번 해설 (2022.08.31 시행) (2) | 2022.09.04 |
| 2023학년도 수능 9월 모의고사 수학 영역 미적분 29, 30번 해설 (2022.08.31 시행) (8) | 2022.08.31 |





댓글 영역