고정 헤더 영역
상세 컨텐츠
본문
사건이 동시에 일어나는 곱의 법칙에 대한 자세한 이해 (고1 수학 경우의 수, 약수 개수, 색칠 문제)

안녕하세요? holymath입니다. 이 카테고리의 포스팅은 2015개정 고등학교 1학년 수학의 개념을 보다 쉽고 자세히 이해할 수 있도록 해설하는 글입니다. 수학을 공부할 때는 공식과 문제 푸는 요령을 외워서 푸는 게 아니라 개념이 만들어진 근본적인 원리와 개념들 사이의 연관성을 생각하면서 공부해야 합니다. 이 포스팅을 통해 교과서나 참고서에 있는 수학 개념을 제대로 이해하는데 도움이 되기를 바랍니다.
지난 포스팅에서 합의 법칙에 대해 공부해 봤죠. 이 포스팅에서는 곱의 법칙의 원리와 다양한 활용 문제를 알아보도록 하겠습니다.

● 곱의 법칙이란?
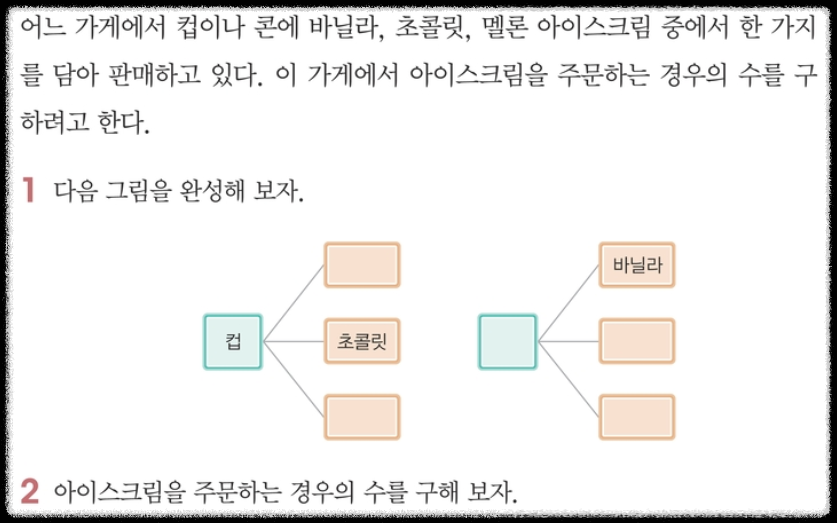
경우의 수는 중학교 2학년 때 기본적인 내용을 공부했다는 걸 지난 포스팅에서 얘기한 바 있어요. 마찬가지로 섬네일에 소개한 예시도 중학교 교과서에 실린 내용입니다. 가게에서 아이스크림을 주문하기 위해 컵이나 콘중에 하나를 선택해야 하고 바닐라, 초콜릿, 멜론 중에 하나를 선택해야 하는 상황입니다.
실생활에서 충분히 경험해 볼 수 있는 상황인데 여기서 나올 수 있는 모든 경우의 수가 6가지인 건 다음의 그림으로부터 쉽게 추측할 수 있어요. 그리고 이 결과는 $2\times 3$의 계산으로부터 구할 수 있습니다.
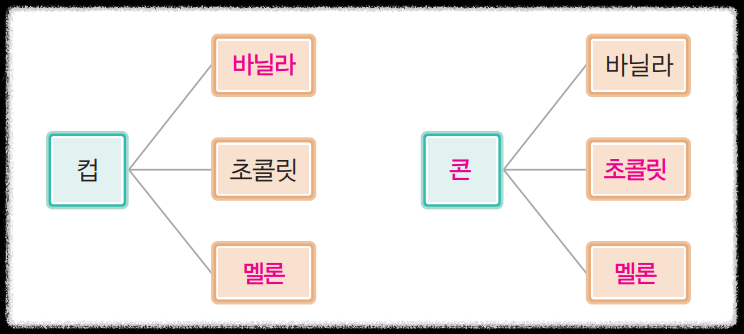
이러한 그림은 나무의 가지가 뻗어나가는 모습과 닮았다고 해서 수형도(樹型圖)라고 부릅니다. 여기서 수(樹)는 나무를 의미하는 한자예요. 이렇게 경우의 수를 구하는 과정에서 선택을 동시에 해야 하는 상황이 일어나면 수형도를 통해 사건을 명확하게 이해할 수 있습니다.
일반적으로 동시에 선택하는 상황이 일어나면 곱셈으로 계산해야 하며 중학교 수학 교과서에서는 다음과 같이 설명합니다.

그리고 아래의 내용이 고등학교에서 설명하는 곱의 법칙입니다.

보다시피 곱의 법칙이라는 용어를 정의한 것과 셋 이상의 사건도 다룰 수 있다는 여지를 준 것 외에는 다를 게 없죠.
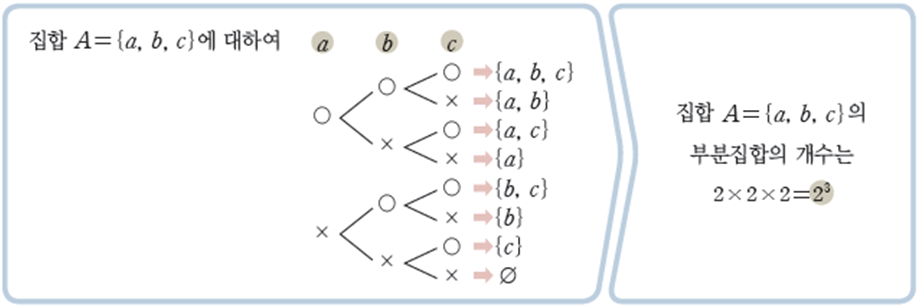
이전에 공부했던 부분집합의 개수를 구하는 원리가 곱의 법칙을 이용한 예시라고 볼 수 있어요.
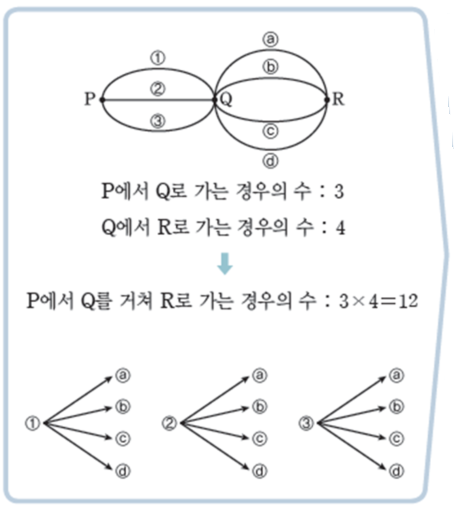
또한, 목적지까지 가기 위해 갈림길에서 길을 선택하는 일이 연달아 일어나는 경우도 다음과 같이 곱의 법칙이 이용됩니다.
● 동시에(잇달아) 일어나는 경우란?
합의 법칙에서는 동시에 일어나지 않는다는 것의 의미를 알아봤는데 곱의 법칙에서 말하는 동시에 일어난다는 개념은 아예 다릅니다.
예를 들어 주사위 하나를 던졌을 때 홀수가 나오는 경우의 수를 A, 소수가 나오는 경우의 수를 B라 할 때 A와 B가 동시에 일어나는 경우의 수는 무엇일까요? 사건 A가 일어나는 경우는 1, 3, 5로 3가지이고, 사건 B가 일어나는 경우는 2, 3, 5로 역시 3가지입니다. 그렇다고 이들을 곱해서 $3\times 3=9$라고 해버리면 완전히 틀린 답이 되죠. A와 B가 동시에 일어나는 상황은 3과 5가 나오는 상황이므로 올바르게 구한 답은 2가 됩니다.
그럼 $3\times 3=9$을 해서 답을 구해야 하는 상황은 어떤 상황이냐? 문제를 다음과 같이 물어본 경우입니다.
| 주사위 A, B를 동시에 던졌을 때 A 주사위에는 홀수가 나오고, B 주사위에는 소수가 나오는 경우의 수를 구하시오. |
위의 질문은 집합 $A=\left\{1,~3,~5\right\}$와 집합 $B=\left\{2,~3,~5\right\}$에 대하여 $\left\{(a,~b)~|~a\in A,~b\in B\right\}$의 원소의 개수를 구하라는 문제와 같은 원리예요. 그래서 문제에서 구하려는 경우의 수를 계산하려면 각각의 경우를 $({\color{Red}1},~2)$, $({\color{Red}1},~3)$, $({\color{Red}1},~5)$, $({\color{Cyan}3},~2)$, $({\color{Cyan}3},~3)$, $({\color{Cyan}3},~5)$, $({\color{Emerald}5},~2)$, $({\color{Emerald}5},~3)$, $({\color{Emerald}5},~5)$와 같이 순서쌍으로 나타냅니다.
즉, 곱의 법칙에서 말하는 두 사건을 동시에 일으킨다는 뜻은 각 사건에서 일어나는 경우를 순서쌍으로 묶는다는 원리가 들어가는 거예요. 그렇게 만들어진 순서쌍을 각각의 경우로 보는 개념이므로 합의 법칙에서 다루었던 두 사건의 교집합을 생각하는 개념과는 다르다는 점에 유의해야 합니다.
실제로 두 집합 $A$, $B$에 대하여 집합 $\left\{(a,~b)~|~a\in A,~b\in B\right\}$를 $A\times B$와 같이 표현하기도 합니다. 같은 맥락으로 집합 $\left\{(a,~b)~|~a\in A,~b\in A\right\}$는 $A^2$와 같이 표현하기도 합니다.
● 약수의 개수 구하기
자연수를 소인수분해하여 약수를 찾는 원리는 중학교 1학년 때 배운 바 있죠. 이때 약수의 개수를 모두 구하는 요령에 곱의 법칙이 사용되는데 교과서의 예제를 먼저 살펴보겠습니다.
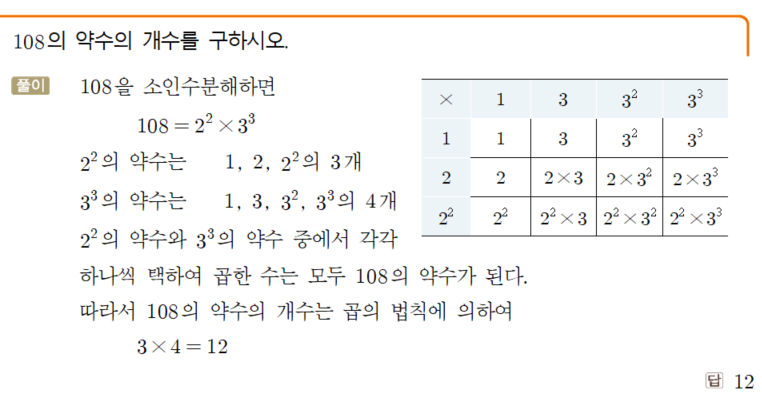
이렇게 표를 이용하면 구하고자 하는 약수를 놓치지 않고 모두 찾아내기 수월하죠. 즉, $108$의 약수는 이 수를 만든 소수인 $2$와 $3$을 몇 개나 사용했는가에 따라 정해지므로 그 개수는 각 소수의 지수가 얼마이냐에 따라 결정됩니다.
이것은 다음과 같이 일반화할 수 있어요.
| ■ 자연수의 약수의 개수 |
| $n$개의 서로 다른 소수 $p_1$, $p_2$, $\cdots$, $p_n$에 대하여 $p_1^{~m_1} p_2^{~m_2} \cdots p_n^{~m_n}$의 약수의 개수는 $(m_1+1) (m_2+1) \cdots (m_n+1)$ 이다. |
예를 들어, $600$의 약수의 개수를 구하기 위해 $600$을 소인수분해하면
$600=2^3\times 3\times 5^2$
$2$는 0개부터 3개까지 선택할 수 있으므로 $3+1=4$가지
$3$은 0개부터 1개까지 선택할 수 있으므로 $1+1=2$가지
$5$는 0개부터 2개까지 선택할 수 있으므로 $2+1=3$가지
따라서 곱의 법칙에 의해 약수의 개수는 $4\times 3\times 2=$ $24$입니다.
● 색칠하는 경우의 수 문제
곱의 법칙을 적용하는 대표적인 예시 중 하나가 색칠문제입니다. 문제집마다 다양하게 색칠 문제가 있으며 좋은책 신사고 교과서에는 색칠 문제에 대한 전용 코너가 존재하는데 다음은 그 내용 중 일부입니다.

영역을 아무거나 택해서 마구잡이로 색칠을 시작하면 위의 대화처럼 난감한 상황에 놓이게 되죠. 색칠 문제에서 중요한 건 가장 많이 인접해 있는 영역을 먼저 칠하는 거예요.
위의 문제에서 (가), (나), (다), (라)와 모두 인접한 (마)부터 먼저 칠하면 고를 수 있는 색깔은 5가지가 되고 (마)에서 택한 색깔은 더 이상 쓸 수 없게 됩니다.
따라서 (가)에서 칠할 수 있는 색깔은 4가지가 되고 이어서 (나)를 색칠한다면 (가)와 (마)에서 칠한 색깔은 선택할 수 없으므로 3가지가 됩니다. (다)에도 마찬가지로 (나)와 (마)에서 칠한 색을 제외한 3가지이에요.
이제 마지막으로 (라)에 들어갈 색이 남았는데 여기서 맹목적으로 2나 3을 곱하면 틀리게 됩니다. (라)에 들어갈 색은 상황에 따라 2가지가 될 수도 있고 3가지가 될 수도 있기 때문이에요. 인접한 영역인 (가), (마), (다)가 모두 다른 색깔이라면 2가지이지만 (가)와 (다)가 같은 색깔이 되는 경우도 있겠죠. 그때는 선택 가능한 색깔이 3가지가 됩니다.
따라서 이 문제는 (가)와 (다)가 같은 색깔이 되는 경우와 다른 색깔이 되는 경우로 나누어서 따로 계산해 주어야 합니다.
1) (가)와 (다)가 같은 색깔인 경우
일단 위에서 알아본 대로 (마), (가), (나)에 차례대로 색을 칠하는 방법의 수는 5, 4, 3입니다. 그리고 (다)에는 (가)에서 정한 색깔을 그대로 따라가야 하므로 색을 칠하는 방법의 수는 1가지입니다. 그리고 마지막으로 (라)에 색을 칠할 방법의 수는 3가지가 되어서 구하는 경우의 수는
$5\times 4\times 3\times 1\times 3=180$
2) (가)와 (다)가 다른 색깔인 경우
(마), (가), (나)에 차례대로 색을 칠하는 방법의 수는 5, 4, 3입니다. 이렇게 세 영역이 모두 다른 색깔로 칠해진 상태에서 (다)에는 세 영역 중 어디와도 색깔이 겹칠 수 없으므로 (다)에 색칠할 수 있는 방법은 2가지가 됩니다. 마지막으로 (라)에는 (가), (마), (다)서 사용한 3가지 색깔을 제외한 나머지 2개 중에 택할 수 있어요. 따라서 구하는 경우의 수는
$5\times 4\times 3\times 2\times 2=240$
1), 2)에 의해 구하는 총경우의 수는 $180+240=$ $420$입니다.
이렇게 상황을 분류하는 경우는 각 상황에서 곱의 법칙이 사용됐지만 마지막에는 합의 법칙이 이용되고 있다는 점도 참고하세요.
● 연습 문제 풀이

$900$의 약수들을 모두 곱한 수를 소인수분해하시오.
$900$을 소인수분해하면
$900=2^2\times 3^2\times 5^2$
따라서 약수의 총개수는 $3\times 3\times 3=27$입니다.
이제 약수들을 모두 곱하면 그 수 또한 $2$, $3$, $5$의 거듭제곱으로 표현될 텐데 각 수가 몇 번이나 곱해졌는지를 알아야 하죠. 이것을 $2$를 기준으로 나눠보겠습니다.
$2$가 하나만 곱해진 약수의 경우 $2\times 3^a\times 5^b$의 꼴이고 $a$와 $b$는 $0$부터 $2$까지의 값을 가질 수 있으므로 역시 곱의 법칙에 의해 $3\times 3=9$가지입니다. 그렇다면 이런 약수 9개를 모두 곱하면 $2$는 총 9번 곱해지게 됩니다.
같은 원리로 $2$가 두 개 곱해진 $2^2\times 3^a\times 5^b$꼴의 약수 또한 9개이므로 모두 곱하면 $2^2$이 총 9번 곱해져요.
따라서 모든 약수를 곱했을 때 2가 곱해진 횟수는 $9\times (1+2)=27$이 됩니다.
$3$과 $5$도 같은 원리로 생각할 수 있으므로 모든 약수를 곱한 결과는 $2^{27}\times 3^{27}\times 5^{27}$입니다.

그림과 같이 6개의 섬이 다리로 연결되어 있다. 흰색, 노란색, 파란색 깃발이 각각 2개씩 총 6개 있을 때, 이 6개의 깃발을 섬에 한 개씩 세우고자 한다. 다리로 연결된 이웃한 두 섬에는 같은 색의 깃발을 세우지 않는다고 할 때, 깃발을 세우는 경우의 수는? (단, 같은 색의 깃발끼리는 서로 구별하지 않는다.) [2017.10월 고3 학평/3점]

① $6$ ② $8$ ③ $10$ ④ $12$ ⑤ $14$
그림의 각 섬에다 번호를 부여해서 단순화시키면 다음과 같습니다.
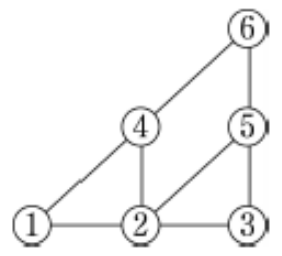
섬이 6개이고 깃발도 6개이므로 6개의 깃발을 모두 사용해야 하는 상황이고 2개의 섬이 같은 색깔로 묶이게 되는 문제예요. 여기서는 ②번 섬을 먼저 고려해 보겠습니다. 이 섬은 4개의 섬과 모두 연결되어 있으므로 ②번 섬과 같은 색깔이 될 수 있는 섬은 ⑥번 밖에 없죠. 이 둘을 같은 그룹으로 묶고 나면 나머지 ①, ③, ④, ⑤번 중에서 같은 색으로 묶을 그룹을 둘로 나눠야 하는데 그 방법이 ①③ / ④⑤로 묶는 방법과 ①⑤ / ③④로 묶는 방법으로 2가지가 있습니다.
즉, 이 문제는 6개의 섬을 두 섬씩 묶어서 3개의 그룹으로 만드는 상황으로 그 방법은 다음과 같이 2가지입니다.
②⑥ / ①③ / ④⑤
②⑥ / ①⑤ / ③④
이렇게 분류하고 나면 3가지의 색을 각 그룹에 색칠하는 방법은 $3\times 2\times 1=6$이죠.
따라서 섬에 깃발을 세우는 총경우의 수는 $2\times 6=12$가 되어 답은 ④번이 됩니다.

집합 $X=\left\{-3,~-2,~-1,~1,~2,~3\right\}$에 대하여 $X$에서 $X$로의 함수 $f(x)$는 다음 조건을 만족시킨다.
| (가) $X$의 모든 원소 $x$에 대하여 $\left|f(x)+f(-x) \right|=1$이다. (나) $x>0$이면 $f(x)>0$이다. |
함수 $f(x)$의 개수를 구하시오. [2016.3월 고3 학평/4점]
조건이 좀 까다로워 보여도 하나씩 체크해 보면 그렇게 복잡하지 않은 문제입니다.
(나) 조건에 의해 $f(1)$의 값이 될 수 있는 건 $1$, $2$, $3$중 하나죠. 그럼 각 경우를 (가) 조건에 대입하여 $f(-1)$의 값이 나올 수 있는 경우를 모두 구하면 됩니다.
1) $f(1)=1$인 경우 $f(-1)=-2$으로 1가지
2) $f(1)=2$인 경우 $f(-1)=-1$ 또는 $f(-1)=-3$ 으로 2가지
3) $f(1)=3$인 경우 $f(-1)=-2$으로 1가지
1), 2), 3)에 의하여 $f(1)$과 $f(-1)$의 값을 정하는 방법의 수는 4가지입니다.
이와 같은 원리로 $f(2)$와 $f(-2)$의 값을 정하는 방법의 수도 4가지이며 마찬가지로 $f(3)$, $f(-3)$의 값을 정하는 경우도 4가지예요.
따라서 곱의 법칙에 의해 함수 $f(x)$의 개수는 $4\times 4\times 4=$ $64$입니다.
♥ 이해가 잘 되셨다면 공감과 선플은 포스팅 강의 제작에 큰 힘이 됩니다.
♥ 이해가 잘 안 되신 부분은 댓글을 통해 질문을 주세요.
♥ 본문의 내용은 추가, 보완될 수 있습니다.

'고1 수학의 남다른 개념 > 경우의 수' 카테고리의 다른 글
| 지불 방법의 수, 지불 금액의 수를 구하는 방법의 자세한 이해 (고1 수학, 경우의 수, 곱의 법칙, 화폐 문제) (2) | 2024.11.17 |
|---|---|
| 수형도를 활용하는 곱의 법칙 문제 풀이 (고1 수학 경우의 수, 모두 다르게 대응하는 디레인지먼트 문제) (6) | 2024.08.21 |
| 최단 거리 경로의 개수를 합의 법칙으로 구하는 법 (고1 수학 경우의 수) (4) | 2024.07.27 |
| 합의 법칙에 대한 자세한 이해 (고1 수학 경우의 수) (2) | 2023.10.10 |





댓글 영역